题目内容
如图,直线l⊥平面α,垂足为O,已知长方体ABCD-A1B1C1D1中,AA1=5,AB=6,AD=8.该长方体做符合以下条件的自由运动:(1)A∈l;(2)C∈α,则C1、O两点间的最大距离为 .
【答案】分析:第一步:找出点A、C、O之间的关系,第二步:找出点C1、P、O之间的关系,第三步:求值,根据直线C1O的长度最长=直线C1P的长度+直线PO的长度进行求解即可.
解答:解:第一步:找出点A、C、O之间的关系
按题意:直线AO垂直于直线CO,三角形AOC为直角三角形,O点在以AC为直径的球面上;
设球面中心点为P,则点P位于直线AC的中点;
第二步:找出点C1、P、O之间的关系 此时答案变为求球外一点至球面上一点的距离;
按题意:存在直角三角形C1CP,直线C1P为斜边(点C1至球心P的距离);
此时:存在任意三角形C1PO,其中直线C1P为点C1至球心P的距离、直线PO为球面半径,直线C1O的长度是我们要的答案
至此,我们可以根据任意三角形一条边与另外两条边的关系可得:直线C1O的长度最长=直线C1P的长度+直线PO的长度
第三步:求值 已知:AB=6,AD=8 则:AC=10,CP= =5 则:PO=
=5 则:PO= =5
=5
(1)已知:AA1=5,CC1=5 则:C1P=(CC12+CP2)0.5=5
(2)C1、O两点间的最大距离=5+5
故答案为:5+5
点评:本题主要考查了空间两点的距离的最值,解题关键是找出垂足O点规律,同时考查了空间想象能力,论证推理能力,属于中档题.
解答:解:第一步:找出点A、C、O之间的关系
按题意:直线AO垂直于直线CO,三角形AOC为直角三角形,O点在以AC为直径的球面上;
设球面中心点为P,则点P位于直线AC的中点;
第二步:找出点C1、P、O之间的关系 此时答案变为求球外一点至球面上一点的距离;
按题意:存在直角三角形C1CP,直线C1P为斜边(点C1至球心P的距离);
此时:存在任意三角形C1PO,其中直线C1P为点C1至球心P的距离、直线PO为球面半径,直线C1O的长度是我们要的答案
至此,我们可以根据任意三角形一条边与另外两条边的关系可得:直线C1O的长度最长=直线C1P的长度+直线PO的长度
第三步:求值 已知:AB=6,AD=8 则:AC=10,CP=
 =5 则:PO=
=5 则:PO= =5
=5 (1)已知:AA1=5,CC1=5 则:C1P=(CC12+CP2)0.5=5

(2)C1、O两点间的最大距离=5+5

故答案为:5+5

点评:本题主要考查了空间两点的距离的最值,解题关键是找出垂足O点规律,同时考查了空间想象能力,论证推理能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
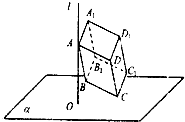 如图,直线l⊥平面α,垂足为O,已知长方体ABCD-A1B1C1D1中,AA1=5,AB=6,AD=8.该长方体做符合以下条件的自由运动:(1)A∈l;(2)C∈α,则C1、O两点间的最大距离为
如图,直线l⊥平面α,垂足为O,已知长方体ABCD-A1B1C1D1中,AA1=5,AB=6,AD=8.该长方体做符合以下条件的自由运动:(1)A∈l;(2)C∈α,则C1、O两点间的最大距离为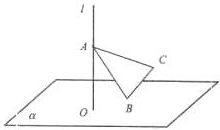 如图,直线l⊥平面α,垂足为O,已知△ABC中,∠ABC为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1)A∈l,(2)B∈α.则C、O两点间的最大距离为
如图,直线l⊥平面α,垂足为O,已知△ABC中,∠ABC为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1)A∈l,(2)B∈α.则C、O两点间的最大距离为 (2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )
(2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( ) (2012•黄州区模拟)如图,直线l⊥平面α,垂足为O,已知在直角三角形ABC中,BC=1,AC=2,AB=
(2012•黄州区模拟)如图,直线l⊥平面α,垂足为O,已知在直角三角形ABC中,BC=1,AC=2,AB=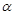 ,垂足为O,已知在直角三角形ABC中, BC=1,AC=2,AB=
,垂足为O,已知在直角三角形ABC中, BC=1,AC=2,AB=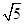 .该直角三角形在空间做符合以下条件的自由运动:(1)
.该直角三角形在空间做符合以下条件的自由运动:(1)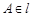 ,(2)
,(2) .则B、O两点间的最大距离为
.
.则B、O两点间的最大距离为
.