题目内容
关于函数
（a为常数，且a＞0）对于下列命题：①函数f（x）的最小值为-1；
②函数f（x）在每一点处都连续；
③函数f（x）在R上存在反函数；
④函数f（x）在x=0处可导；
⑤对任意的实数x1＜0，x2＜0且x1＜x2，恒有
其中正确命题的序号是 ．
【答案】分析：①只需说明在点x=0处函数f（x）的最小值是-1；
②函数在点x=0处两段都有意义且函数值都为-1，故②正确
③函数f（x）在R上不是单调函数
④只需说明在x=0时，两段导函数都有意义且函数值相等；
⑤已知函数在R上先增后减，所以f（x）的图象在[0，+∞）上是上凸的，所以任取两点连线应在图象的上方
解答：解：①由题意可得函数在x＜0时单调递减，在x＞0时单调递增，在点x=0处函数f（x）的最小值是-1，故①正确
②只需说明在点x=0处连续，只需说明在x=0时，两段都有意义且函数值相等；
③函数f（x）在R上不是单调函数，故不存在反函数，故③错误
④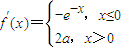
，故④错误
⑤函数在R上先增后减，所以f（x）的图象在[0，+∞）上是上凸的，所以任取两点连线应在图象的上方，故⑤正确
故答案为：①②⑤
点评：连续就是函数图象不间断，在x=0可导就是导函数在两段导函数都有意义且函数值相等，函数在某一区间上不单调，就不会有导函数，利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值，结合函数图象，知下凸的函数图象，任取两点连线应在图象的上方．
②函数在点x=0处两段都有意义且函数值都为-1，故②正确
③函数f（x）在R上不是单调函数
④只需说明在x=0时，两段导函数都有意义且函数值相等；
⑤已知函数在R上先增后减，所以f（x）的图象在[0，+∞）上是上凸的，所以任取两点连线应在图象的上方
解答：解：①由题意可得函数在x＜0时单调递减，在x＞0时单调递增，在点x=0处函数f（x）的最小值是-1，故①正确
②只需说明在点x=0处连续，只需说明在x=0时，两段都有意义且函数值相等；
③函数f（x）在R上不是单调函数，故不存在反函数，故③错误
④
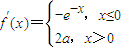，故④错误⑤函数在R上先增后减，所以f（x）的图象在[0，+∞）上是上凸的，所以任取两点连线应在图象的上方，故⑤正确
故答案为：①②⑤
点评：连续就是函数图象不间断，在x=0可导就是导函数在两段导函数都有意义且函数值相等，函数在某一区间上不单调，就不会有导函数，利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值，结合函数图象，知下凸的函数图象，任取两点连线应在图象的上方．
练习册系列答案
相关题目
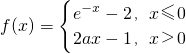（a为常数，且a＞0）对于下列命题：
（a为常数，且a＞0），对于下列命题：
；
）＜
；
（a为常数，且a＞0）对于下列命题：
（a为常数，且a>0）对于下列命题：
.