题目内容
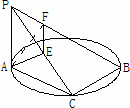
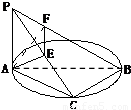
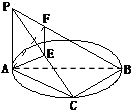如图PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，E、F分别是点A在PB、PC上的射影，给出下列结论：
①AF⊥PB ②AE⊥平面PBC ③AF⊥BC ④EF⊥PB ⑤二面角A-PB-C的平面角是∠AFE，
其中真命题的序号是________．
①②④⑤
分析：利用射影的定义、直径所对的圆周角为直角等知识判定线线垂直，AF⊥PB，AE⊥PB，BC⊥AC．然后利用线线垂直?线面垂直?面面垂直的相互转化关系判定即可
解答：∵F是点A在PB上的射影，∴AF⊥PB，①√；
∵PA⊥⊙O所在平面，∴PA⊥BC，∵AB是⊙O的直径，∴BC⊥AC，∴BC⊥平面PAC，∴AE⊥BC，又∵AE⊥PC
∴AE⊥平面PBC，故②√；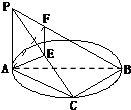
∵假设AF⊥BC，则AF⊥平面PBC，又∵AE⊥平面PBC，∴E、F重合，与已知矛盾．∴③×；
∵AE⊥平面PBC，∴AE⊥PB，又PB⊥AF，∴PB⊥平面AEF，∴EF⊥PB，故④√；
∵PB⊥平面AEF，∴∠AFE是二面角A-PB-C的平面角，故⑤√；
故答案是①②④⑤
点评：本题考查空间中垂直关系的判定，要准确把握线线垂直?线面垂直?面面垂直相互转化的条件．
分析：利用射影的定义、直径所对的圆周角为直角等知识判定线线垂直，AF⊥PB，AE⊥PB，BC⊥AC．然后利用线线垂直?线面垂直?面面垂直的相互转化关系判定即可
解答：∵F是点A在PB上的射影，∴AF⊥PB，①√；
∵PA⊥⊙O所在平面，∴PA⊥BC，∵AB是⊙O的直径，∴BC⊥AC，∴BC⊥平面PAC，∴AE⊥BC，又∵AE⊥PC
∴AE⊥平面PBC，故②√；
∵假设AF⊥BC，则AF⊥平面PBC，又∵AE⊥平面PBC，∴E、F重合，与已知矛盾．∴③×；
∵AE⊥平面PBC，∴AE⊥PB，又PB⊥AF，∴PB⊥平面AEF，∴EF⊥PB，故④√；
∵PB⊥平面AEF，∴∠AFE是二面角A-PB-C的平面角，故⑤√；
故答案是①②④⑤
点评：本题考查空间中垂直关系的判定，要准确把握线线垂直?线面垂直?面面垂直相互转化的条件．
练习册系列答案
相关题目
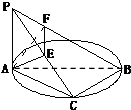如图PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，E、F分别是点A在PB、PC上的射影，给出下列结论：
