题目内容
函数f（x）=-2x2+7x-6与函数g（x）=-x的图象所围成的封闭图形的面积为
- A.
- B.2
- C.
- D.3
C
分析：先将两函数联立求得两图象的交点坐标，以确定积分区间，再根据图象和定积分的几何意义确定被积函数为f（x）-g（x），最后利用微积分基本定理计算定积分即可得面积
解答：由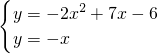
得
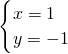和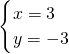
∴函数f（x）=-2x2+7x-6与函数g（x）=-x的图象所围成的封闭图形的面积S=∫13（f（x）-g（x））dx=∫13（-2x2+8x-6）dx
=（-x3+4x2-6x）|13=（-18+36-18）-（-+4-6）=
故选C
点评：本题考查了定积分的几何意义和运算性质，微积分基本定理及其应用
分析：先将两函数联立求得两图象的交点坐标，以确定积分区间，再根据图象和定积分的几何意义确定被积函数为f（x）-g（x），最后利用微积分基本定理计算定积分即可得面积
解答：由
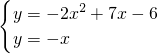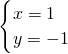得和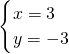∴函数f（x）=-2x2+7x-6与函数g（x）=-x的图象所围成的封闭图形的面积S=∫13（f（x）-g（x））dx=∫13（-2x2+8x-6）dx
=（-
x3+4x2-6x）|13=（-18+36-18）-（-+4-6）=故选C
点评：本题考查了定积分的几何意义和运算性质，微积分基本定理及其应用
练习册系列答案
相关题目
设函数f（x）=
，则满足f（x）=4的x的值是（ ）
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |