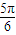题目内容
已知z=（1-2sinθ）+（2cosθ+
）i（0＜θ＜π）是纯虚数，则θ=（ ）
| 3 |
分析：利用一个复数为纯虚数的条件是实部等于0，虚部不等于0，求出θ 角的三角函数值满足的条件，进而求出此角．
解答：解：∵z=（1-2sinθ）+2（cosθ+
）i是纯虚数，0＜θ＜π，∴1-2sinθ=0，2（cosθ+
）≠0，
∴sinθ=
，cosθ≠-
，∴θ=
，
故选 A．
| 3 |
| 3 |
∴sinθ=
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
故选 A．
点评：本题考查一个复数为实数的条件是实部等于0，虚部不等于0，以及由角的三角函数值求角．
练习册系列答案
相关题目
已知z（1-i）=1，则复数z在复平面上对应的点位于（ ）
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |
）i（0＜θ＜π）是纯虚数，则θ=
）i（0＜θ＜π）是纯虚数，则θ=（ ）
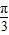
或
）i（0＜θ＜π）是纯虚数，则θ=（ ）
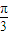
或