题目内容
若直线l1：2x+3y-6=0和直线l2：4x+6y+a=0之间的距离为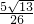
，则a=________．
-7或-17
分析：因为两平行线的距离已知，可在一条直线上取一点坐标，然后利用点到直线的距离公式求出这点到另一条直线的距离d，让d等于平行线间的距离即可列出关于a的方程，求出方程的解即可得到a的值．
解答：在直线l1：2x+3y-6=0取一点坐标（3，0）
∵直线l1和l2之间的距离为，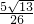
∴点（3，0）的直线l2的距离d=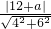
=，
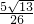∴|12+a|=5，
∴a=-7或-17．
故答案为：-7或-17
点评：此题考查学生灵活运用点到直线的距离公式化简求值，理解平行线间的距离即为一条直线上的一个点到另外一条直线的距离，是一道基础题．
分析：因为两平行线的距离已知，可在一条直线上取一点坐标，然后利用点到直线的距离公式求出这点到另一条直线的距离d，让d等于平行线间的距离即可列出关于a的方程，求出方程的解即可得到a的值．
解答：在直线l1：2x+3y-6=0取一点坐标（3，0）
∵直线l1和l2之间的距离为
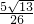，∴点（3，0）的直线l2的距离d=
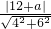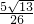=，∴|12+a|=5，
∴a=-7或-17．
故答案为：-7或-17
点评：此题考查学生灵活运用点到直线的距离公式化简求值，理解平行线间的距离即为一条直线上的一个点到另外一条直线的距离，是一道基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若直线l1：2x+（m+1）y+4=0与直线l2：mx+3y-2=0平行，则m的值为（ ）
| A、-2 | B、-3 | C、2或-3 | D、-2或-3 |