题目内容
抛物线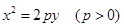 过焦点F的直线
过焦点F的直线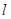 交抛物线于A、B两点,O为原点,若
交抛物线于A、B两点,O为原点,若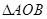 面积最小值为8。
面积最小值为8。
(1)求P值
(2)过A点作抛物线的切线交y轴于N,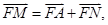 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。
【答案】
⑴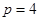 ⑵
⑵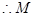 点在直线
点在直线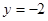 上
上
【解析】(1)设出直线方程,注意斜率是否存在,然后直线方程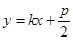 与抛物线
与抛物线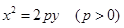 联立,消去
联立,消去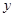 整理得一元二次方程,利用根与系数的关系把
整理得一元二次方程,利用根与系数的关系把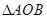 面积用
面积用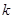 和
和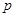 表示,分析
表示,分析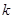 的范围求出最小值为8,得
的范围求出最小值为8,得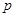 的值;(2)由导数的几何意义求出过A点的抛物线的切线方程,得到切线与
的值;(2)由导数的几何意义求出过A点的抛物线的切线方程,得到切线与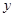 轴的交点
轴的交点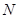 ,设出点
,设出点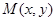 ,根据
,根据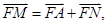 可找到点
可找到点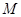 的横纵坐标
的横纵坐标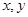 用点
用点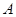 的横纵坐标
的横纵坐标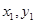 表示,就证出点M在一定直线上
表示,就证出点M在一定直线上
⑴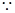 抛物线
抛物线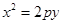 的焦点
的焦点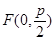
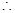 设直线
设直线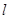 方程为
方程为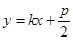
由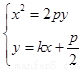 消去
消去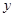 得
得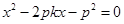 设
设
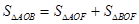
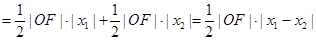
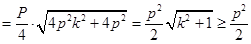 当
当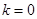 的等号成立
的等号成立 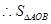 面积的最小值为
面积的最小值为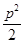
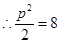
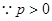
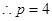 (7分)
(7分)
⑵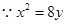
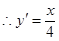
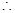 过A点的切线方程为
过A点的切线方程为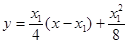
即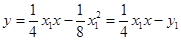
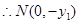 设
设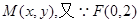
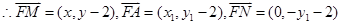
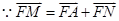
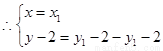 得
得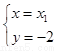
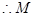 点在直线
点在直线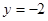 上
上

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 设抛物线M方程为y2=2px(p>0),其焦点为F,P(a,b)(a≠0)为直线y=x与抛物线M的一个交点,|PF|=5
设抛物线M方程为y2=2px(p>0),其焦点为F,P(a,b)(a≠0)为直线y=x与抛物线M的一个交点,|PF|=5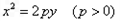 过焦点F的直线l交抛物线于A.B两点,O为原点,若△AOB面积最小值为8。
过焦点F的直线l交抛物线于A.B两点,O为原点,若△AOB面积最小值为8。 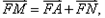 则点M在一定直线上,试证明之。
则点M在一定直线上,试证明之。