题目内容
10.函数y=sin($\frac{π}{2}$-2015x)是( )| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
分析 根据诱导公式和余弦函数的性质即可判断.
解答 解:y=sin($\frac{π}{2}$-2015x)=cos2015x,
∴函数为偶函数,
故选:B.
点评 本题考查了函数的奇偶性,余弦函数的性质,诱导公式,属于基础题.

练习册系列答案
相关题目
20.对于a,b∈R,定义运算“?”:$a?b=\left\{{\begin{array}{l}{{a^2}-ab,a≤b}\\{{b^2}-ab,a>b}\end{array}}\right.$,设f(x)=(2x-1)?(x-1),且关于x的方程f(x)=t(t∈R)恰有三个互不相等的实数根x1,x2,x3,则x1+x2+x3的取值范围是( )
| A. | $(\frac{{5-\sqrt{3}}}{4},1)$ | B. | $(1,\frac{{5+\sqrt{3}}}{4})$ | C. | $(\frac{1}{2},1)$ | D. | (1,2) |
19.已知函数f(x)=(x-1)3+2014(x-1),等差数列{an}的前n项和为Sn,且f(a2)+f(a2014)=0,则S2015=( )
| A. | 4030 | B. | 4028 | C. | 2015 | D. | 2014 |
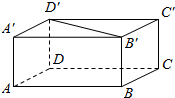 已知:如图的长方体AC′,求证:B′D′∥平面ABCD.
已知:如图的长方体AC′,求证:B′D′∥平面ABCD.