题目内容
如图,已知△OFP的面积为m,且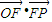 =1.
=1.(I)若
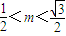 ,求向量
,求向量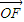 与
与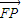 的夹角θ的取值范围;
的夹角θ的取值范围;(II)设
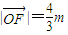 ,且
,且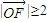 .若以O为中心,F为焦点的椭圆经过点P,当
.若以O为中心,F为焦点的椭圆经过点P,当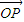 取得最小值时,求此椭圆的方程.
取得最小值时,求此椭圆的方程.
【答案】分析:(1)根据△OFP的面积为m,设向量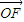 与
与 的夹角为θ,因为
的夹角为θ,因为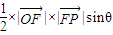 =m,
=m, ×
×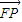 =1,
=1,
∴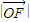 •
•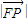 cosθ=1,可得tanθ=2m,进而可得答案.
cosθ=1,可得tanθ=2m,进而可得答案.
(2)以O为原点,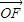 所在直线为x轴建立直角坐标系,设
所在直线为x轴建立直角坐标系,设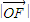 =c,P点坐标为(x,y),所以
=c,P点坐标为(x,y),所以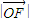 =
= m
m
 •
•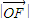 •|y|=
•|y|=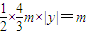 ,即
,即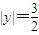 .因为
.因为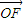 =(c,0),
=(c,0),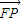 =(x-c,y),
=(x-c,y),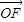 •
•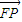 =1
=1
所以
所以可得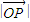 =
=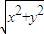 =
=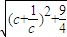 ,
,
设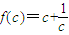 ,判断知f(c)在[2,+∞)上是增函数.
,判断知f(c)在[2,+∞)上是增函数.
所以当c=2时,f(c)为最小,从而 为最小,此时P(
为最小,此时P(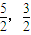 ).
).
最终得到答案.
解答:解:(I)∵△OFP的面积为m,设向量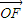 与
与 的夹角为θ.
的夹角为θ.
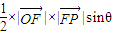 =m ①
=m ①
∵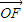 ×
×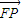 =1,∴
=1,∴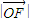 •
•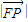 cosθ=1 ②
cosθ=1 ②
由①、②得:tanθ=2m
∵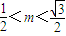 ,∴
,∴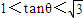 ,∴
,∴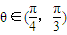
即向量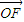 与
与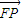 的夹角θ的取值范围为
的夹角θ的取值范围为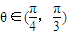
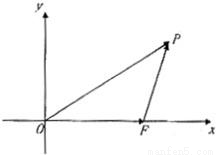 (II)如图,以O为原点,
(II)如图,以O为原点,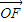 所在直线为x轴建立直角坐标系
所在直线为x轴建立直角坐标系
设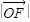 =c,P点坐标为(x,y)∵
=c,P点坐标为(x,y)∵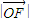 =
= m
m
∴ •
•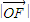 •|y|=
•|y|=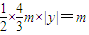 ,∴
,∴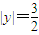
∵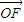 =(c,0),
=(c,0),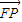 =(x-c,y),
=(x-c,y),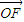 •
• =1
=1
∴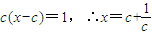
∴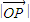 =
=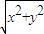 =
=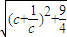
设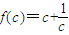 ,当c≥2时,任取c2>c1≥2
,当c≥2时,任取c2>c1≥2
有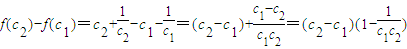
当c2>c1≥2时,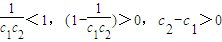
∴f(c2)-f(c1)>0,∴f(c)在[2,+∞)上是增函数
∴当c=2时,f(c)为最小,从而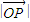 为最小,此时P(
为最小,此时P( )
)
设椭圆的方程为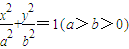 ,则
,则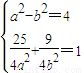 ∴a2=10,b2=6
∴a2=10,b2=6
故椭圆的方程为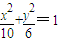 .
.
点评:本题主要考查向量的数量积运算和椭圆的标准方程的求法.属难题.
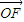 与
与 的夹角为θ,因为
的夹角为θ,因为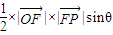 =m,
=m, ×
×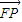 =1,
=1,∴
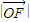 •
•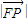 cosθ=1,可得tanθ=2m,进而可得答案.
cosθ=1,可得tanθ=2m,进而可得答案.(2)以O为原点,
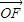 所在直线为x轴建立直角坐标系,设
所在直线为x轴建立直角坐标系,设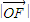 =c,P点坐标为(x,y),所以
=c,P点坐标为(x,y),所以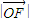 =
= m
m •
•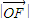 •|y|=
•|y|=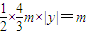 ,即
,即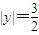 .因为
.因为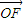 =(c,0),
=(c,0),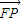 =(x-c,y),
=(x-c,y),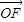 •
•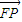 =1
=1所以

所以可得
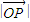 =
=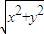 =
=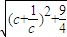 ,
,设
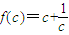 ,判断知f(c)在[2,+∞)上是增函数.
,判断知f(c)在[2,+∞)上是增函数.所以当c=2时,f(c)为最小,从而
 为最小,此时P(
为最小,此时P(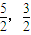 ).
).最终得到答案.
解答:解:(I)∵△OFP的面积为m,设向量
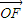 与
与 的夹角为θ.
的夹角为θ.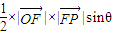 =m ①
=m ①∵
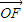 ×
×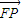 =1,∴
=1,∴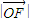 •
•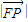 cosθ=1 ②
cosθ=1 ②由①、②得:tanθ=2m
∵
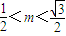 ,∴
,∴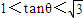 ,∴
,∴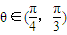
即向量
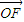 与
与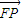 的夹角θ的取值范围为
的夹角θ的取值范围为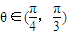
 (II)如图,以O为原点,
(II)如图,以O为原点,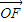 所在直线为x轴建立直角坐标系
所在直线为x轴建立直角坐标系设
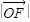 =c,P点坐标为(x,y)∵
=c,P点坐标为(x,y)∵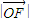 =
= m
m∴
 •
•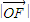 •|y|=
•|y|=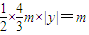 ,∴
,∴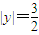
∵
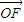 =(c,0),
=(c,0),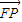 =(x-c,y),
=(x-c,y),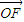 •
• =1
=1∴
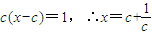
∴
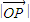 =
=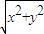 =
=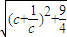
设
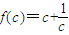 ,当c≥2时,任取c2>c1≥2
,当c≥2时,任取c2>c1≥2有
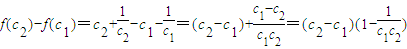
当c2>c1≥2时,
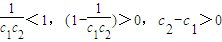
∴f(c2)-f(c1)>0,∴f(c)在[2,+∞)上是增函数
∴当c=2时,f(c)为最小,从而
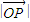 为最小,此时P(
为最小,此时P( )
)设椭圆的方程为
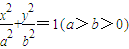 ,则
,则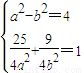 ∴a2=10,b2=6
∴a2=10,b2=6故椭圆的方程为
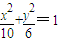 .
.点评:本题主要考查向量的数量积运算和椭圆的标准方程的求法.属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
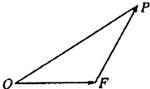 如图,已知△OFP的面积为m,且
如图,已知△OFP的面积为m,且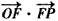 =1,
=1,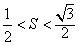 ,求向量
,求向量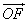 与
与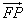 的夹角θ的取值范围;
的夹角θ的取值范围;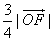 且
且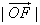 ≥2,当
≥2,当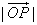 取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。
取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。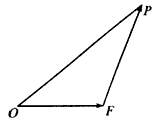
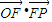 =1.
=1.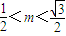 ,求向量
,求向量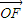 与
与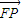 的夹角θ的取值范围;
的夹角θ的取值范围;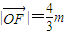 ,且
,且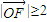 .若以O为中心,F为焦点的椭圆经过点P,当
.若以O为中心,F为焦点的椭圆经过点P,当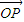 取得最小值时,求此椭圆的方程.
取得最小值时,求此椭圆的方程.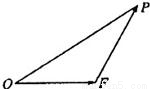
 =1.
=1. ,求向量
,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围; ,且
,且 .若以O为中心,F为焦点的椭圆经过点P,当
.若以O为中心,F为焦点的椭圆经过点P,当 取得最小值时,求此椭圆的方程.
取得最小值时,求此椭圆的方程.