题目内容
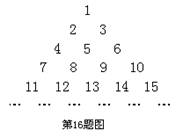
 如图,将全体正整数排成一个三角数阵,根据规律,数阵中第n行的从左到右的第3个数是
如图,将全体正整数排成一个三角数阵,根据规律,数阵中第n行的从左到右的第3个数是| n2-n+6 |
| 2 |
| n2-n+6 |
| 2 |
分析:根据题意,可以归纳出:第n行有n个数(n≥3),且每行从左到右为公差为1的等差数列,可得前n行共有1+2+3+4+…+n=
个数,进而可得答案.
| n(n+1) |
| 2 |
解答:解:根据题意,分析所给的数阵可得,第n行有n个数(n≥3),且每行从左到右为公差为1的等差数列,
则前n行共有1+2+3+4+…+n=
个数,
则第n行从左向右的第1个数是
+1,
则第n行从左向右的第3个数是
+3=
,
故答案为:
.
则前n行共有1+2+3+4+…+n=
| n(n+1) |
| 2 |
则第n行从左向右的第1个数是
| (n-1)n |
| 2 |
则第n行从左向右的第3个数是
| (n-1)n |
| 2 |
| n2-n+6 |
| 2 |
故答案为:
| n2-n+6 |
| 2 |
点评:本题考查归纳推理的运用,关键在于发现数阵中各行数的变化规律.

练习册系列答案
相关题目

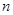 行
行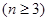 从左向右的第
从左向右的第 个数为
个数为
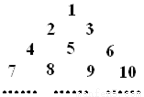
 .
.