题目内容
已知椭圆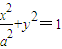 (a>0)的离心率为
(a>0)的离心率为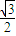 .
.(1)求椭圆的方程;
(2)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为(-a,0),若|AB|=
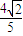 ,求直线l的倾斜角.
,求直线l的倾斜角.
【答案】分析:(1)根据离心率得出3a2=4c2以及c2=a2-b2,求出a、b的值;
(2)由A(-2,0),设B(x1,y1),直线l的方程为y=k(x+2),知A、B两点的坐标满足方程组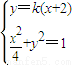 ,由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0,由-2x1=
,由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0,由-2x1=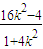 得x1=
得x1=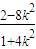 ,从而y1=
,从而y1=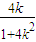 ,再由|AB|=
,再由|AB|=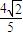 ,求出k的值,即可得到倾斜角.
,求出k的值,即可得到倾斜角.
解答:解:(1)由e=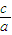 =
=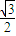 ,得3a2=4c2.再由c2=a2-b2,解得a=2b=2.
,得3a2=4c2.再由c2=a2-b2,解得a=2b=2.
所以椭圆的方程为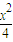 +y2=1.(4分)
+y2=1.(4分)
(2)由(1)可知点A的坐标是(-2,0).设点B的坐标为(x1,y1),
直线l的斜率为k.则直线l的方程为y=k(x+2).
于是A、B两点的坐标满足方程组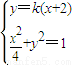 消去y并整理,
消去y并整理,
得:(1+4k2)x2+16k2x+16k2-4=0
由-2x1=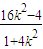 得x1=
得x1=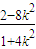 ,从而y1=
,从而y1=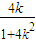 .(6分)
.(6分)
所以|AB|= =
=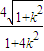 .
.
由|AB|=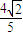 ,得
,得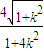 =
=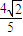
整理得32k4-9k2-23=0,即(k2-1)(32k2+23)=,解得k=±1.
经检验△>0符合题意,所以直线l的倾斜角为 或
或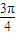 .(12分)
.(12分)
点评:本题考查椭圆方程的求法和直线与圆锥曲线问题,解题时要认真审题,注意挖掘题设中的隐条件,属于难题.
(2)由A(-2,0),设B(x1,y1),直线l的方程为y=k(x+2),知A、B两点的坐标满足方程组
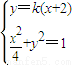 ,由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0,由-2x1=
,由方程消去y并整理得:(1+4k2)x2+16k2x+16k2-4=0,由-2x1=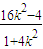 得x1=
得x1=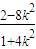 ,从而y1=
,从而y1=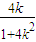 ,再由|AB|=
,再由|AB|=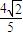 ,求出k的值,即可得到倾斜角.
,求出k的值,即可得到倾斜角.解答:解:(1)由e=
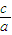 =
=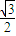 ,得3a2=4c2.再由c2=a2-b2,解得a=2b=2.
,得3a2=4c2.再由c2=a2-b2,解得a=2b=2.所以椭圆的方程为
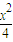 +y2=1.(4分)
+y2=1.(4分)(2)由(1)可知点A的坐标是(-2,0).设点B的坐标为(x1,y1),
直线l的斜率为k.则直线l的方程为y=k(x+2).
于是A、B两点的坐标满足方程组
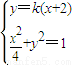 消去y并整理,
消去y并整理,得:(1+4k2)x2+16k2x+16k2-4=0
由-2x1=
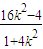 得x1=
得x1=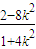 ,从而y1=
,从而y1=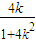 .(6分)
.(6分)所以|AB|=
 =
=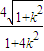 .
.由|AB|=
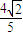 ,得
,得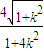 =
=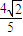
整理得32k4-9k2-23=0,即(k2-1)(32k2+23)=,解得k=±1.
经检验△>0符合题意,所以直线l的倾斜角为
 或
或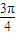 .(12分)
.(12分)点评:本题考查椭圆方程的求法和直线与圆锥曲线问题,解题时要认真审题,注意挖掘题设中的隐条件,属于难题.

练习册系列答案
相关题目
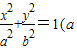 >b>0)的离心率为
>b>0)的离心率为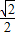 ,且过点
,且过点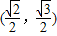 .
.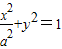 (a>0)的离心率为
(a>0)的离心率为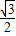 .
.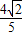 ,求直线l的倾斜角.
,求直线l的倾斜角. (a>0)的离心率为
(a>0)的离心率为 .
. ,求直线l的倾斜角.
,求直线l的倾斜角.