题目内容
如果将函数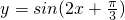 的图象向右平移φ(φ>0)个单位,所得的函数图象关于直线
的图象向右平移φ(φ>0)个单位,所得的函数图象关于直线 对称,则φ的最小值为
对称,则φ的最小值为
- A.

- B.

- C.

- D.

A
分析:先求得函数平移后函数的解析式,进而根据对称轴所在的函数值为最大或最小,进而求得2( -φ)+
-φ)+ =kπ+
=kπ+ 求出φ的值.
求出φ的值.
解答:函数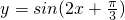 的图象向右平移φ(φ>0)个单位,得y=sin[2(x-φ)+
的图象向右平移φ(φ>0)个单位,得y=sin[2(x-φ)+
∵函数图象关于直线 对称,
对称,
∴2( -φ)+
-φ)+ =kπ+
=kπ+ 求得φ=-
求得φ=- +
+
∵φ>0
∴φ的最小值为
故选A
点评:本题主要考查了三角函数的图象的变换和三角函数的对称性问题.考查了考生对三角函数基础知识的掌握.
分析:先求得函数平移后函数的解析式,进而根据对称轴所在的函数值为最大或最小,进而求得2(
 -φ)+
-φ)+ =kπ+
=kπ+ 求出φ的值.
求出φ的值.解答:函数
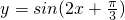 的图象向右平移φ(φ>0)个单位,得y=sin[2(x-φ)+
的图象向右平移φ(φ>0)个单位,得y=sin[2(x-φ)+
∵函数图象关于直线
 对称,
对称,∴2(
 -φ)+
-φ)+ =kπ+
=kπ+ 求得φ=-
求得φ=- +
+
∵φ>0
∴φ的最小值为

故选A
点评:本题主要考查了三角函数的图象的变换和三角函数的对称性问题.考查了考生对三角函数基础知识的掌握.

练习册系列答案
相关题目
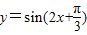 的图象向右平移φ(φ>0)个单位,所得的函数图象关于直线
的图象向右平移φ(φ>0)个单位,所得的函数图象关于直线 对称,则φ的最小值为( )
对称,则φ的最小值为( )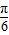
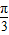
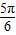
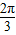
 的图象向右平移
的图象向右平移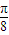 个单位得到函数y=g(x)的图象,则函数y=g(x)的解析式为 .
个单位得到函数y=g(x)的图象,则函数y=g(x)的解析式为 .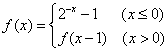 ,若方程
,若方程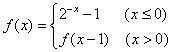 ,若方程
,若方程