题目内容
已知关于x的函数y=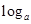 (2-ax)在[0,1]上是减函数,则a的取值范围是
(2-ax)在[0,1]上是减函数,则a的取值范围是
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)]
【答案】
B
【解析】
试题分析:因为关于x的函数y=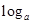 (2-ax)在[0,1]上是减函数,而a>0,u=2-ax是减函数,所以y=
(2-ax)在[0,1]上是减函数,而a>0,u=2-ax是减函数,所以y=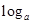 u是增函数,因此,a>1且2-a×1>0,1<a<2,故选B。
u是增函数,因此,a>1且2-a×1>0,1<a<2,故选B。
考点:本题主要考查复合对数函数的单调性。
点评:易错题,复合函数的单调性判定方法是:内外层函数的单调性“同增异减”。该题要注意对数的真数大于零。

练习册系列答案
相关题目
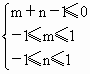 ,求函数y=mx+n的图象经过一、二、三象限的概率.
,求函数y=mx+n的图象经过一、二、三象限的概率.