题目内容
下列说法错误的序号是(1)“sinθ=
| 1 | 2 |
(2)命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”
(3)若命题p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1≥0;
(4)如果命题“?p”与命题“p或q”都是真命题,那么命题q一定是真命题.
分析:通过解三角方程求出)“sinθ=
”?θ=2kπ+
或θ=2kπ+
,判断出(1)错;
根据否命题的形式判断出(2)对;根据含量词的命题的否定,判断出(3)对;根据复合命题的真假判断出(4)对.
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
根据否命题的形式判断出(2)对;根据含量词的命题的否定,判断出(3)对;根据复合命题的真假判断出(4)对.
解答:解:对于(1),若)“sinθ=
”?θ=2kπ+
或θ=2kπ+
,
所以“sinθ=
”“θ=30°不一定成立,反之当“θ=30°成立,“sinθ=
”一定成立,故(1)错;
对于(2)“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,故(2)对;
对于(3)命题p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1≥0,故(3)对;
对于(4)“?p”为真命题,则p为假命题,又“p或q”是真命题,所以q为真命题,故(4)对.
故答案为(1)
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
所以“sinθ=
| 1 |
| 2 |
| 1 |
| 2 |
对于(2)“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,故(2)对;
对于(3)命题p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1≥0,故(3)对;
对于(4)“?p”为真命题,则p为假命题,又“p或q”是真命题,所以q为真命题,故(4)对.
故答案为(1)
点评:判断一个命题是另一个命题的什么条件,应该先化简各个命题,再利用充要条件的有关定义进行判断.

练习册系列答案
相关题目
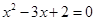 ,则
,则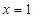 ”的逆否命题是“若
”的逆否命题是“若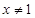 ,则
,则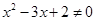 ”;
”;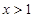 ”是“
”是“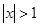 ”的充分不必要条件;
”的充分不必要条件;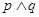 ”为假命题,则
”为假命题,则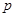 、
、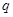 均为假命题;
均为假命题; ,使得
,使得 ,则
,则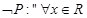 ,均有
,均有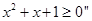 ;
; 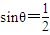 ”是“θ=30°”的充分不必要条件;
”是“θ=30°”的充分不必要条件;