题目内容
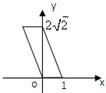
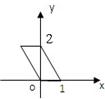
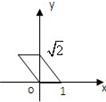
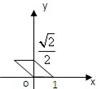
用斜二测画法画一个边长为2的正三角形的直观图,则此直观图面积的为 .
分析:根据斜二测画法与平面直观图的关系进行求解即可.
解答: 解:如图△A'B'C'是边长为2的正三角形ABC的直观图,则A'B'=2,C'D'为正三角形ABC的高CD的一半,即C'D'=
解:如图△A'B'C'是边长为2的正三角形ABC的直观图,则A'B'=2,C'D'为正三角形ABC的高CD的一半,即C'D'=
×
=
,
则高C'E=C'D'sin45°=
×
=
,
∴三角形△A'B'C'的面积为
×2×
=
.
故答案为:
.
 解:如图△A'B'C'是边长为2的正三角形ABC的直观图,则A'B'=2,C'D'为正三角形ABC的高CD的一半,即C'D'=
解:如图△A'B'C'是边长为2的正三角形ABC的直观图,则A'B'=2,C'D'为正三角形ABC的高CD的一半,即C'D'=| 1 |
| 2 |
| 3 |
| ||
| 2 |
则高C'E=C'D'sin45°=
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
∴三角形△A'B'C'的面积为
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题主要考查斜二测画法的应用,要求熟练掌握斜二测对应边长的对应关系,比较基础.

练习册系列答案
相关题目
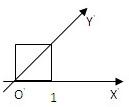 如图:用斜二测画法画一个水平放置的平面图形是一个边长为1的正方形,则原来图形的形状是( )
如图:用斜二测画法画一个水平放置的平面图形是一个边长为1的正方形,则原来图形的形状是( )