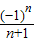题目内容
若数列的前4项分别是
,-
,
,-
,则此数列的一个通项公式为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
分析:根据数列的前4项可得,奇数项为负数,偶数项为正数,第n项的绝对值等于|
|,由此可得此数列的一个通项公式为
.
| 1 |
| n+1 |
| (-1)n+1 |
| n+1 |
解答:解:根据数列的前4项分别是
,-
,
,-
,可得奇数项为负数,偶数项为正数,第n项的绝对值等于|
|,
故此数列的一个通项公式为
,
故答案为
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n+1 |
故此数列的一个通项公式为
| (-1)n+1 |
| n+1 |
故答案为
| (-1)n+1 |
| n+1 |
点评:本题主要考查数列的概念及其简单表示法,求数列的通项公式,属于基础题.注意通项公式不是唯一的,如
也是此数列的一个通项公式.
| (-1)n-1 |
| n+1 |

练习册系列答案
相关题目
 ,则此数列的一个通项公式为
,则此数列的一个通项公式为



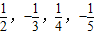 ,则此数列的一个通项公式为( )
,则此数列的一个通项公式为( )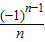



 ,则此数列的一个通项公式为( )
,则此数列的一个通项公式为( )



 ,则此数列的一个通项公式为( )
,则此数列的一个通项公式为( )