题目内容
定义域R的函数f(x)满足f(x+2)=3f(x),当x∈[0,2]时,f(x)=x2-2x,若x∈[-4,-2]时,f(x)≥
(
-t)恒成立,则实数t的取值范围是( )
| 1 |
| 18 |
| 3 |
| t |
| A、(-∞,-1]∪(0,3] | ||||
B、(-∞,-
| ||||
| C、[-1,0)∪[3,+∞) | ||||
D、[-
|
分析:(1)由x∈[0,2]时,f(x)=x2-2x及f(x+2)=3f(x)可求得f(x+4)=(x+4)2-2(x+4)=x2+6x+8,从而可得
f(x)=
(x2+6x+8),x∈[-4,-2],而x∈[-4,-2]时,f(x)≥
(
-t)恒成立可转化为
(
-t)≤f(x)min,结合二次函数的知识可先求函数f(x)的最小值,从而可求t的范围
f(x)=
| 1 |
| 9 |
| 1 |
| 18 |
| 3 |
| t |
| 1 |
| 18 |
| 3 |
| t |
解答:解:∵x∈[-4,-2]
∴x+4∈[0,2]
∵x∈[0,2]时,f(x)=x2-2x
∴f(x+4)=(x+4)2-2(x+4)=x2+6x+8
∵函数f(x)满足f(x+2)=3f(x)
∴f(x+4)=3f(x+2)=9f(x)
∴f(x)=
(x2+6x+8),x∈[-4,-2]
∵x∈[-4,-2]时,f(x)≥
(
-t)恒成立
(
-t)≤f(x)min=-
解不等式可得t≥3或-1≤t<0
故选C.
∴x+4∈[0,2]
∵x∈[0,2]时,f(x)=x2-2x
∴f(x+4)=(x+4)2-2(x+4)=x2+6x+8
∵函数f(x)满足f(x+2)=3f(x)
∴f(x+4)=3f(x+2)=9f(x)
∴f(x)=
| 1 |
| 9 |
∵x∈[-4,-2]时,f(x)≥
| 1 |
| 18 |
| 3 |
| t |
| 1 |
| 18 |
| 3 |
| t |
| 1 |
| 9 |
解不等式可得t≥3或-1≤t<0
故选C.
点评:解决本题的关键在于“转化”,先将恒成立问题转化为求解函数的最小值问题,再结合二次函数在闭区间上的最值问题,最终得以解决.很多问题在实施“化难为易”、“化生为熟”中得以解决.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )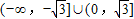
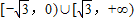
 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )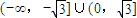

 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )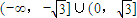
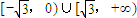
 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
