题目内容
已知椭圆C的中心为直角坐标系xOy的原点，焦点在x轴上，它的一个顶点到两个焦点的距离分别是7和1（1）求椭圆C的方程；
（2）若P为椭圆C的动点，M为过P且垂直于x轴的直线上的点，
| OP | |OM| |
分析：（1）根据题意，椭圆的一个顶点到两个焦点的距离分别是7和1，分析可得这个顶点是长轴的端点，则有a+c=7，a-c=1；解可得ac的值，进而可得b的值，即可得答案；
（2）设M（x，y），P（x，y1 ），根据椭圆的方程为
+
=1且P在椭圆上，可得e的值与y12=
①；根据题意，有
=e2=
②；联立①②化简可得答案．
（2）设M（x，y），P（x，y1 ），根据椭圆的方程为
| x2 |
| 16 |
| y2 |
| 7 |
| 7(16-x2) |
| 16 |
x2+
| ||
| x2+y2 |
| 9 |
| 16 |
解答：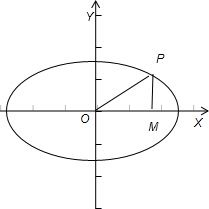
解：（1）根据题意，椭圆的一个顶点到两个焦点的距离分别是7和1，
则这个顶点不会是短轴的端点，而是长轴的端点，
则有a+c=7，a-c=1；
解可得a=4，c=3；
则b=
；
故椭圆的方程为
+
=1；
（2）设M（x，y），P（x，y1 ），
椭圆的方程为
+
=1中，e=
=
；
又由椭圆方程为
+
=1，且P在椭圆上，即y12=
①；
根据题意得
=e2=
②；
①②联立化简可得，y2=
；
即y=±
，（-4≤x≤4）
其轨迹是两条平行于x轴的线段．
解：（1）根据题意，椭圆的一个顶点到两个焦点的距离分别是7和1，则这个顶点不会是短轴的端点，而是长轴的端点，
则有a+c=7，a-c=1；
解可得a=4，c=3；
则b=
| 7 |
故椭圆的方程为
| x2 |
| 16 |
| y2 |
| 7 |
（2）设M（x，y），P（x，y1 ），
椭圆的方程为
| x2 |
| 16 |
| y2 |
| 7 |
| c |
| a |
| 3 |
| 4 |
又由椭圆方程为
| x2 |
| 16 |
| y2 |
| 7 |
| 7(16-x2) |
| 16 |
根据题意得
x2+
| ||
| x2+y2 |
| 9 |
| 16 |
①②联立化简可得，y2=
| 112 |
| 9 |
即y=±
4
| ||
| 3 |
其轨迹是两条平行于x轴的线段．
点评：本题考查椭圆的性质与轨迹的求法，实际是椭圆的综合题目，注意轨迹方程的求法步骤，尤其是轨迹与轨迹方程的区别与联系．
练习册系列答案
相关题目
与椭圆交于A，B两点，
的面积为4，
的周长为