题目内容
已知定义在正实数集R上的函数y=f(x)满足:①对任意a,b∈R都有f(a•b)=f(a)+f(b)②当x>1时,f(x)<0 ③f(3)=-1
(1)求f(1)的值
(2)证明函数y=f(x)在R上为单调减函数
(3)若集合A={(p,q)|f(p2+1)-f(5q)-2>0,p,q∈R+},集合B={(p,q)|f( )+
)+ =0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.
=0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.
解:(1)令a=1,b=1,∵f(a•b)=f(a)+f(b);
∴f(1)=f(1)+f(1)
∴f(1)=0
(2)证明,设a,b为任意正实数,且0<a<b,
∴ >1.
>1.
∴f( )=f(b)+f(
)=f(b)+f( ),
),
∵f(1)=f(x)+f( )=0
)=0
∴f(x)=-f( );
);
∴f( )=f(b)+f(
)=f(b)+f( )=f(b)-f(a)<0;
)=f(b)-f(a)<0;
即f(b)<f(a);
故函数y=f(x)在R上为单调减函数.
(3)解∵f(p2+1)-f(5q)-2>0,由(2)知f(x)=-f( );
);
∴f(p2+1)+f(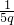 )>2;
)>2;
∴f(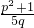 )>2;
)>2;
又f(3)=-1,
∴f( )=1
)=1
∴f(9)=-2;
∴f( )=2;
)=2;
∴f(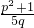 )>2=f(
)>2=f( );
);
∴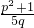 <
< ①
①
又∵f( )+
)+ =0;
=0;
∴f( )+
)+ f(
f( )=0;
)=0;
f( )+f(
)+f( )=0;
)=0;
∴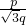 =1,p=
=1,p= q; ②
q; ②
由①②整理得:27q2-5q+9<0不成立,
∴不存在p,q,使A∩B≠∅.
分析:(1)直接令a=1,b=1代入f(a•b)=f(a)+f(b)即可得到结论;
(2)先根据f(a•b)=f(a)+f(b)得到f(x)=-f( );再结合x>1时,f(x)<0以及单调性的定义即可得到答案;
);再结合x>1时,f(x)<0以及单调性的定义即可得到答案;
(3)先分别利用f(3)=-1把两个集合进行转化,再结合一元二次不等式的解法即可得出结论.
点评:本题考点是抽象函数及其应用,考查用赋值法求函数值,以及灵活利用所给的恒等式证明函数的单调性,此类题要求答题者有较高的数学思辨能力,属于较高难度的题目.
∴f(1)=f(1)+f(1)
∴f(1)=0
(2)证明,设a,b为任意正实数,且0<a<b,
∴
 >1.
>1.∴f(
 )=f(b)+f(
)=f(b)+f( ),
),∵f(1)=f(x)+f(
 )=0
)=0∴f(x)=-f(
 );
);∴f(
 )=f(b)+f(
)=f(b)+f( )=f(b)-f(a)<0;
)=f(b)-f(a)<0;即f(b)<f(a);
故函数y=f(x)在R上为单调减函数.
(3)解∵f(p2+1)-f(5q)-2>0,由(2)知f(x)=-f(
 );
);∴f(p2+1)+f(
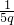 )>2;
)>2;∴f(
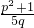 )>2;
)>2;又f(3)=-1,
∴f(
 )=1
)=1∴f(9)=-2;
∴f(
 )=2;
)=2;∴f(
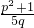 )>2=f(
)>2=f( );
);∴
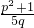 <
< ①
①又∵f(
 )+
)+ =0;
=0;∴f(
 )+
)+ f(
f( )=0;
)=0;f(
 )+f(
)+f( )=0;
)=0;∴
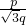 =1,p=
=1,p= q; ②
q; ②由①②整理得:27q2-5q+9<0不成立,
∴不存在p,q,使A∩B≠∅.
分析:(1)直接令a=1,b=1代入f(a•b)=f(a)+f(b)即可得到结论;
(2)先根据f(a•b)=f(a)+f(b)得到f(x)=-f(
 );再结合x>1时,f(x)<0以及单调性的定义即可得到答案;
);再结合x>1时,f(x)<0以及单调性的定义即可得到答案;(3)先分别利用f(3)=-1把两个集合进行转化,再结合一元二次不等式的解法即可得出结论.
点评:本题考点是抽象函数及其应用,考查用赋值法求函数值,以及灵活利用所给的恒等式证明函数的单调性,此类题要求答题者有较高的数学思辨能力,属于较高难度的题目.

练习册系列答案
相关题目
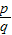 )+
)+ =0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.
=0,p,q∈R+},问是否存在p,q,使A∩B≠∅,若存在,求出p,q的值,不存在则说明理由.