题目内容

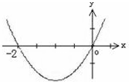函数y=f′（x）的图象如图所示，则f（x）的解析式可能是（　　）
分析：首先观察函数的图象，y=f′（x）与x轴的交点即为f（x）的极值点，然后可得导函数解析式，从而求出函数f（x）的解析式，得到正确选项．
解答：解：由图可以看出函数y=f′（x）在x=0和-2点为0，
故可设y=f′（x）=ax（x+2）=ax2+2ax
∴f（x）=
1
3
ax3+ax2+b
取a=1，b=0即为选项B，满足条件，其它选项不满足条件．
故选：B．
点评：会观察函数的图象并从中提取相关信息，并熟练掌握函数与其导数的关系，属于基础题．
练习册系列答案
相关题目
先作函数y=lg
1
1-x
的图象关于原点对称的图象，再将所得图象向右平移一个单位得图象C1，又函数y=f（x）的图象C2与C1关于直线y=x对称，则函数y=f（x）的解析式是（　　）
已知函数y=f（x）的定义域为（-1，1），并且对一切x，y∈（-1，1）恒有f（x）+f（y）=f（x+y）；且当x＞0时，f（x）＜0；
（1）判断该函数的奇偶性；
（2）判断并证明该函数的单调性；
（3）若f（1-m）+f（1-m2）＞0，求实数m的取值范围．
（2012•青岛二模）已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图示．
x -1 0 4 5
f（x） 1 2 2 1
下列关于f（x）的命题：
①函数f（x）的极大值点为0，4；
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点；
⑤函数y=f（x）-a的零点个数可能为0、1、2、3、4个．
其中正确命题的序号是
①②⑤
①②⑤
．
给出定义：若m-
1
2
＜x≤m+
1
2
（其中m为整数），则m叫做离实数x最近的整数，记作{x}，即{x}=m．在此基础上给出下列关于函数f（x）=|x-{x}|的四个命题：
①函数y=f（x）的定义域是R，值域是[0，
1
2
]；
②函数y=f（x）的图象关于直线x=
k
2
（k∈Z）对称；
③函数y=f（x）是周期函数，最小正周期是1；
则其中真命题是
①②③
①②③
．
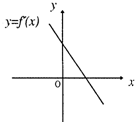函数y=f（x）的图象过原点且它的导函数y=f'（x）的图象是如图所示的一条直线，y=f（x）的图象的顶点在（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网