题目内容
(1)求函数y=x(a-2x)(x>0,a为大于2x的常数)的最大值;(2)设x>-1,求函数y=
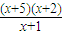 的最值.
的最值.
【答案】分析:(1)(2)两题皆可以利用均值不等式定理进行求解.
解答:解:(1)∵x>0,a>2x,
∴y=x(a-2x)= ×2x(a-2x)
×2x(a-2x)
≤ ×[
×[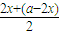 ]2
]2
=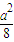 ,
,
当且仅当x=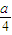 时取等号,故函数的最大值为
时取等号,故函数的最大值为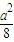 .
.
(2)∵x>-1,∴x+1>0,
设x+1=z>0,则x=z-1,
∴y=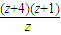 =
=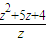 =z+
=z+ +5
+5
≥2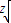 +5=9,
+5=9,
当且仅当z=2即x=1时上式取等号,
∴x=1时,函数y有最小值9,无最大值.
点评:均值不等式定理要求必须满足“一正,二定,三相等”.
解答:解:(1)∵x>0,a>2x,
∴y=x(a-2x)=
 ×2x(a-2x)
×2x(a-2x)≤
 ×[
×[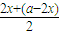 ]2
]2=
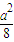 ,
,当且仅当x=
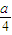 时取等号,故函数的最大值为
时取等号,故函数的最大值为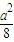 .
.(2)∵x>-1,∴x+1>0,
设x+1=z>0,则x=z-1,
∴y=
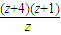 =
=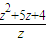 =z+
=z+ +5
+5≥2
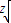 +5=9,
+5=9,当且仅当z=2即x=1时上式取等号,
∴x=1时,函数y有最小值9,无最大值.
点评:均值不等式定理要求必须满足“一正,二定,三相等”.

练习册系列答案
相关题目