题目内容
我们用min{S1,S2,…,Sn}和max{S1,S2,…,Sn}分别表示实数S1,S2,…,Sn中的最小者和最大者.
(1)设f(x)=min{sinx,cosx},g(x)=max{sinx,cosx},x∈[0,2π],函数f(x)的值域为A,函数g(x)的值域为B,求A∩B;
(2)数学课上老师提出了下面的问题:设a1,a2,an为实数,x∈R,求函数![]() (x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数
(x1<x2<xn∈R=的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数![]() 和
和![]() 的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
的最值.学生甲得出的结论是:[f(x)]min=min{f(-2),f(-1),f(1)},且f(x)无最大值.学生乙得出的结论是:[g(x)]max=max{g(-1),g(1),g(2)},且g(x)无最小值.请选择两个学生得出的结论中的一个,说明其成立的理由;
(3)试对老师提出的问题进行研究,写出你所得到的结论并加以证明(如果结论是分类的,请选择一种情况加以证明).
答案:
解析:
解析:
(1)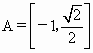 ,
,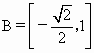 ,∴
,∴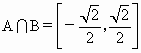 . 4分
. 4分
(2)若选择学生甲的结论,则说明如下,
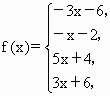
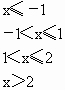 ,于是
,于是![]() 在区间
在区间![]() 上是减函数,在
上是减函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,在
上是增函数,在![]() 上是增函数. 8分
上是增函数. 8分
所以函数![]() 的最小值是
的最小值是![]() ,且函数
,且函数![]() 没有最大值. 10分
没有最大值. 10分
若选择学生乙的结论,则说明如下,
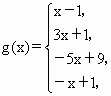
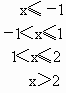 ,于是
,于是![]() 在区间
在区间![]() 上是增函数,在
上是增函数,在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是减函数.
上是减函数.
所以函数![]() 的最大值是
的最大值是![]() ,且函数
,且函数![]() 没有最小值. 10分(3)结论:
没有最小值. 10分(3)结论:
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]()
![]() ;
;
若![]() ,则
,则![]() ,
,
![]()
![]()
(写出每个结论得1分,共3分,证明为5分)
以第一个结论为例证明如下:
∵![]() ,∴当
,∴当![]() 时,
时,
![]() ,是减函数,
,是减函数,
当![]() 时,
时,
![]() ,是增函数
,是增函数
当![]() 时,函数
时,函数![]() 的图像是以点
的图像是以点![]() ,
,![]() ,
,![]()
为端点的一系列互相连接的折线所组成,
所以有![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目