题目内容
求三数324，243，270的最大公约数.
解法一：324=243×1+81，
243=81×3+0.
则324与243的最大公约数为a=81.
又270=81×3+27，
81=27×3+0,
则324，243，270的最大公约数为27.
解法二：(324，243，270)→(81，54，27)→(27，54，27)→(27，27，27).
所以，324，243，270的最大公约数为27.
243=81×3+0.
则324与243的最大公约数为a=81.
又270=81×3+27，
81=27×3+0,
则324，243，270的最大公约数为27.
解法二：(324，243，270)→(81，54，27)→(27，54，27)→(27，27，27).
所以，324，243，270的最大公约数为27.
欲求三数的最大公约数，可先求两数的最大公约数a，然后求a与第三个数的最大公约数b，则b为所求的三数的最大公约数.
练习册系列答案
相关题目
当x=-2时的值
的
和
的最大公约数是（ ）
11，则输出的数等于
＋2
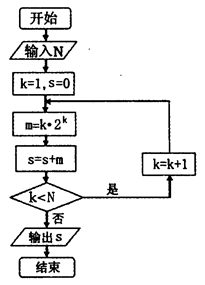
－2