题目内容
定义区间[x1,x2](x1<x2)的长度为x2-x1,已知函数y= |log| 1 | 2 |
分析:先对函数化简可得,y= |log
x|=
,做出函数的简图,结合图象可知要使得函数的值域为[0,2]则函数定义域的最大区间为[
,4],从而可求
| 1 |
| 2 |
|
| 1 |
| 4 |
解答: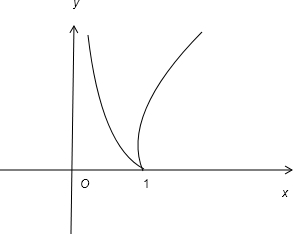 解:∵y= |log
解:∵y= |log
x|的值域为[0,2]
∴0≤|log
x|≤2
∴0≤log
x≤2或-2≤log
x≤0
∴
≤x≤1或1≤x≤4即
≤x≤4
∵定义域为[a,b]时函数的值域[0,2],
由图象可知,定义域大区间的最大值为4-
=
,区间的最小值1-
=
,其差为3
故答案为:3
 解:∵y= |log
解:∵y= |log| 1 |
| 2 |
∴0≤|log
| 1 |
| 2 |
∴0≤log
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 4 |
∵定义域为[a,b]时函数的值域[0,2],
由图象可知,定义域大区间的最大值为4-
| 1 |
| 4 |
| 15 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
故答案为:3
点评:本题主要考查了对数函数的定义域及函数的值域的求解,体现了数形结合的思想的应用.

练习册系列答案
相关题目