题目内容
6.直线l经过抛物线y2=4x焦点F,且与抛物线相交于A(x1,y1),B(x2,y2)两点,通过点A和抛物线顶点的直线交抛物线的准线于点D.(I)若直线l的斜率为1,求线段AB的长;
(Ⅱ)求证:直线DB平行于抛物线的对称轴.
分析 (I)抛物线y2=4x的焦点F(1,0),准线方程为x=-1,由题意可得直线AB的方程为y=x-1,联立方程可得x2-6x+1=0,根据方程的根与系数的关系可得,xA+xB=6,xA•xB=1,由抛物线的定义可知,AB=AF+BF=xA+1+xB+1,代入可求
(Ⅱ)设A(x1,y1),B(x2,y2).直线OA的方程为:y=$\frac{{y}_{1}}{{x}_{1}}$x=$\frac{4}{{y}_{1}}$x,令x=-1,可得yD=-$\frac{4}{{y}_{1}}$.设直线AB的方程为:my=x-1,与抛物线的方程联立化为y2-4m-4=0,利用根与系数的关系可得y1y2=-4,可得yD=y2.即可证明.
解答 (I)解:抛物线y2=4x的焦点F(1,0),准线方程为x=-1
∴直线AB的方程为y=x-1
联立方程y2=4x可得x2-6x+1=0
∴xA+xB=6,xA•xB=1
由抛物线的定义可知,AB=AF+BF=xA+1+xB+1=xA+xB+2=8
(Ⅱ)证明:设A(x1,y1),B(x2,y2).
直线OA的方程为:y=$\frac{{y}_{1}}{{x}_{1}}$x=$\frac{4}{{y}_{1}}$x,令x=-1,可得yD=-$\frac{4}{{y}_{1}}$.
设直线AB的方程为:my=x-1,
联立方程y2=4x,化为y2-4m-4=0,
∴y1y2=-4.
∴y2=-$\frac{4}{{y}_{1}}$
∴yD=y2.
∴直线DB平行于抛物线的对称轴.
点评 本题主要考查了直线与抛物线的位置关系:相交关系的应用,方程的根系数的关系的应用,体现了抛物线的定义的灵活应用.考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
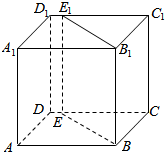 如图,过正方体ABCD-A1B1C1D1的棱BB1的平面交DD1C1C于EE1.求证:BB1∥EE1.
如图,过正方体ABCD-A1B1C1D1的棱BB1的平面交DD1C1C于EE1.求证:BB1∥EE1. 张明拿着一个罐子来找陈华玩,罐子里有四个一样大小的玻璃球,两个黑色,两个白色.张明说:使劲摇晃罐子,使罐中的小球位置打乱,等小球落定后,如果是黑白相间地排列(如图所示)就算甲方赢,否则就算乙方赢,试问陈华要当甲方还是乙方,请你给陈华出个主意.
张明拿着一个罐子来找陈华玩,罐子里有四个一样大小的玻璃球,两个黑色,两个白色.张明说:使劲摇晃罐子,使罐中的小球位置打乱,等小球落定后,如果是黑白相间地排列(如图所示)就算甲方赢,否则就算乙方赢,试问陈华要当甲方还是乙方,请你给陈华出个主意.