题目内容
下列命题中是假命题的是( )
| A、?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上递减 | B、?a>0,函数f(x)=ln2x+lnx-a有零点 | C、?α,β∈R,使cos(α+β)=cosα+sinβ | D、?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 |
分析:A中由幂函数的定义m-1=0,求出f(x),再判在(0,+∞)上的单调性即可;
B中函数f(x)=ln2x+lnx-a有零点?方程ln2x+lnx=a有解,转化为求y=ln2x+lnx的值域问题;
C和D中可用特值
B中函数f(x)=ln2x+lnx-a有零点?方程ln2x+lnx=a有解,转化为求y=ln2x+lnx的值域问题;
C和D中可用特值
解答:解:A中由幂函数的定义m-1=0,所以f(x)=x-1,在(0,+∞)上递减正确;
B中函数f(x)=ln2x+lnx-a有零点?方程ln2x+lnx=a有解,而y=ln2x+lnx∈[-
,+∞)
故a∈[-
,+∞),所以结论正确;
C中取α=
,β=0时成立,故正确;
D中φ=
时,函数f(x)=sin(2x+φ)=cos(2x),是偶函数,故错误
故选D
B中函数f(x)=ln2x+lnx-a有零点?方程ln2x+lnx=a有解,而y=ln2x+lnx∈[-
| 1 |
| 4 |
故a∈[-
| 1 |
| 4 |
C中取α=
| 3π |
| 2 |
D中φ=
| π |
| 2 |
故选D
点评:本题考查幂函数的定义、单调性、函数的零点、三角函数公式及性质等知识,考查知识点较多,但难度不大.

练习册系列答案
相关题目

 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件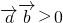 “是“
“是“ 的夹角为锐角”的充要条件
的夹角为锐角”的充要条件 ”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件
”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0垂直”的充要条件