题目内容
设
，
是互相垂直的单位向量，向量
=（m+1）
-3
，
=
-（m-1）
，（
+
）⊥（
-
），则实数m为（ ）
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、-
| ||
| D、不存在 |
分析：根据两个向量垂直的条件，得到两个向量的数量积为零，在参与运算的向量中
，
是互相垂直的单位向量，则数量积的结果最后只含要求的变量m，解方程即可．
| i |
| j |
解答：解：∵
，
是互相垂直的单位向量
又∵（
+
）•（
-
）
=[（m+2）
+（m-4）
]•[m
-（m+2）
]
=（m+2）m-（m-4）（m+2）=4m+8=0，
∴m=-2．
故选A．
| i |
| j |
又∵（
| a |
| b |
| a |
| b |
=[（m+2）
| i |
| j |
| i |
| j |
=（m+2）m-（m-4）（m+2）=4m+8=0，
∴m=-2．
故选A．
点评：启发学生在理解数量积的运算特点的基础上，逐步把握数量积的运算律，引导学生注意数量积性质的相关问题的特点，以熟练地应用数量积的性质．?
练习册系列答案
相关题目
设
，
是互相垂直的单位向量，向量
=(m+1)
-3
，
=
+(m-1)
．若(
+
)⊥(
-
)，则实数m的值是（ ）
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| a |
| b |
A、-
| ||
| B、2 | ||
C、
| ||
| D、-2 |
D.不存在
=（m+1）
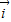-3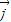
，
=
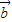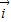-（m-1）
，（
+
）⊥（
-
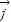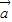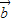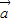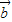），则实数m为（ ）
=（m+1）
-3
，
=
-（m-1）
，（
+
）⊥（
-
），则实数m为（ ）