题目内容
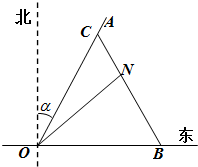 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中tanα=
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中tanα=| 1 |
| 3 |
| 3 |
| 5 |
(1)求S关于p的函数关系;
(2)当p为何值时,抢救最及时?
分析:(1)由已知中射线OA行驶(北偏东α角),其中tanα=
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中sinβ=
.我们可能建立直角坐标系,分别求出直线的方程和点的坐标,进而可以得到S关于p的函数关系;
(2)p为何值时,抢救最及时,可转化为求函数的最小值,根据(1)中的函数解析式,利用基本不等式,可求出函数的最小值,进而得到答案.
| 1 |
| 3 |
| 3 |
| 5 |
(2)p为何值时,抢救最及时,可转化为求函数的最小值,根据(1)中的函数解析式,利用基本不等式,可求出函数的最小值,进而得到答案.
解答: 解:(1)建立如图所示的直角坐标系,
解:(1)建立如图所示的直角坐标系,
∵ON=5a,sinβ=
,∴sin∠BON=
,cos∠BON=
,∴N点的坐标为(3a,4a).
又射线OA的方程为y=3x,
又B(p,0),∴直线BN的方程为
=
(p≠3a)
∴y=
(x-p),(x≠3a).…(4分)
当p=3a时,C(3a,9a),S=
•3a•9a=
a2.
当p≠3a时,方程组
,解为
(p>
a)
∴点C的坐标为(
,
)(p>
a).
∴S=
•|OB|•|yc|=
p•
=
(p>
a).对p=3a也成立.
∴S=
(p>
a).…(8分)
(2)由(1)得S=
=
(p>
a).
令p-
a=t>0,∴S=
=2a(t+
+
a)≥
a2,
当且仅当t=
,即t=
,此时p=
,上式取等号,∴当p=
Km时,S有最小值,即抢救最及时.…(14分)
 解:(1)建立如图所示的直角坐标系,
解:(1)建立如图所示的直角坐标系,∵ON=5a,sinβ=
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
又射线OA的方程为y=3x,
又B(p,0),∴直线BN的方程为
| y-0 |
| 4a-0 |
| x-p |
| 3a-p |
∴y=
| 4a |
| 3a-p |
当p=3a时,C(3a,9a),S=
| 1 |
| 2 |
| 27 |
| 2 |
当p≠3a时,方程组
|
|
| 5 |
| 3 |
∴点C的坐标为(
| 4ap |
| 3p-5a |
| 12ap |
| 3p-5a |
| 5 |
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 12ap |
| 3p-5a |
| 6ap2 |
| 3p-5a |
| 5 |
| 3 |
∴S=
| 6ap2 |
| 3p-5a |
| 5 |
| 3 |
(2)由(1)得S=
| 6ap2 |
| 3p-5a |
| 2ap2 | ||
p-
|
| 5 |
| 3 |
令p-
| 5 |
| 3 |
2a(
| ||
| t |
| 25a2 |
| 9t |
| 10 |
| 3 |
| 40 |
| 3 |
当且仅当t=
| 25a2 |
| 9t |
| 5a |
| 3 |
| 10a |
| 3 |
| 10a |
| 3 |
点评:本题考查的知识点是函数模型的选择与应用,其中解答的关键是建立平面直角坐标系,将题目中的相关直线、点的方程或坐标具体化,进而拟合出函数模型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.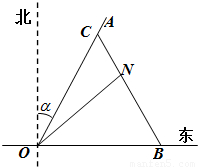 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中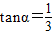 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中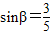 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.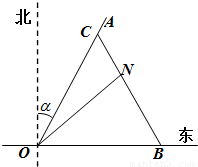 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中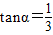 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中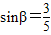 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.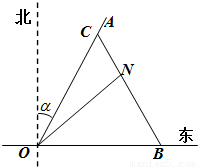 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中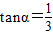 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中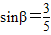 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.