题目内容
4. 淮北市政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A为顶点、AD为对称轴的抛物线的一段曲线段.
淮北市政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A为顶点、AD为对称轴的抛物线的一段曲线段.(1)若QP=x,阴影部分的面积为S,用x表示S的解析式;
(2)试求该高科技工业园区的最大面积.
分析 (1)如图所示建立平面直角坐标系,从而写出各点的坐标,从而可得|EQ|=4-x2,|RP|=x+4-x2,|QP|=x,从而求得;
(2)求导S′=-3x2+x+4=(-3x+4)(x+1),从而可得当x=$\frac{4}{3}$时,有最大面积S=-$\frac{{4}^{3}}{{3}^{3}}$+$\frac{\frac{{4}^{2}}{{3}^{2}}}{2}$+4×$\frac{4}{3}$=$\frac{104}{27}$.
解答 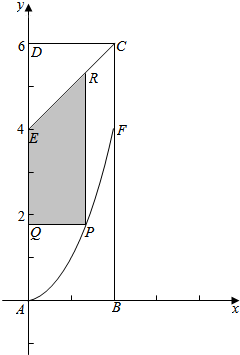 解:(1)如图所示建立平面直角坐标系,如右图,
解:(1)如图所示建立平面直角坐标系,如右图,
A(0,0),B(2,0),C(2,6),
D(0,6),E(0,4),F(2,4),
易知抛物线的方程为y=x2,
由QP=x,(0<x<2),点P(x,x2);
直线CE的方程为y=x+4,
故点R(x,x+4);
故|EQ|=4-x2,|RP|=x+4-x2,|QP|=x,
故S=$\frac{1}{2}$(4-x2+x+4-x2)•x=-x3+$\frac{{x}^{2}}{2}$+4x;
(2)∵S=-x3+$\frac{{x}^{2}}{2}$+4x,
∴S′=-3x2+x+4=(-3x+4)(x+1),
∴S在(0,$\frac{4}{3}$)上是增函数,在($\frac{4}{3}$,2)上是减函数,
故当x=$\frac{4}{3}$时,有最大面积S=-$\frac{{4}^{3}}{{3}^{3}}$+$\frac{\frac{{4}^{2}}{{3}^{2}}}{2}$+4×$\frac{4}{3}$=$\frac{104}{27}$;
故该高科技工业园区的最大面积为$\frac{104}{27}$km2.
点评 本题考查了函数在实际问题中的应用,同时考查了导数的综合应用.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{6}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{21}{25}$ | D. | $\frac{24}{25}$ |
| A. | 5 | B. | 30 | C. | 31 | D. | 32 |
| A. | 若x2+y2=0,则x≠0且y≠0 | B. | 若x2+y2=0,则x≠0或y≠0 | ||
| C. | 若x2+y2≠0,则x≠0且y≠0 | D. | 若x2+y2≠0,则x≠0或y≠0 |
 如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点.
如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点.