题目内容
已知不等式(m +4m-5)x
+4m-5)x -4(m-1)x+3>0对一切实数x恒成立,求实数m的取值范围。
-4(m-1)x+3>0对一切实数x恒成立,求实数m的取值范围。
[1,19)
解析试题分析:根据题意,由于不等式(m +4m-5)x
+4m-5)x -4(m-1)x+3>0对一切实数x恒成立,那么当m
-4(m-1)x+3>0对一切实数x恒成立,那么当m +4m-5=0,m=-5(舍),m=1,显然成立,故可知当m=1成立;m
+4m-5=0,m=-5(舍),m=1,显然成立,故可知当m=1成立;m +4m-5
+4m-5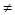 0,则开口向上,判别式小于零即可,得到1<m<19,综上可知满足题意的实数m的取值范围[1,19)。
0,则开口向上,判别式小于零即可,得到1<m<19,综上可知满足题意的实数m的取值范围[1,19)。
考点:不等式的恒成立
点评:本题考查二次函数的取值范围,是基础题.解题时要认真审题,注意分类讨论思想的灵活运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
设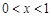 ,函数
,函数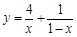 的最小值为( )
的最小值为( )
| A.10 | B.9 | C.8 | D.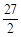 |
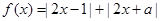 ,
,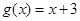 .
. 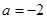 时,求不等式
时,求不等式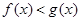 的解集;
的解集;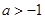 ,且当
,且当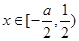 时,
时,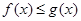 ,求
,求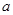 的取值范围。
的取值范围。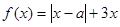 ,其中
,其中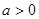 .
.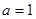 时,求不等式
时,求不等式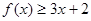 的解集;
的解集; 的解集为
的解集为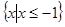 ,求
,求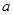 的值.
的值.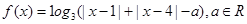 。
。 的解集;
的解集;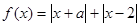
 的解集
的解集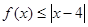 的解集包含[1,2],求
的解集包含[1,2],求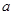 的取值范围
的取值范围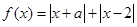
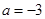 时,求不等式
时,求不等式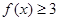 的解集;
的解集;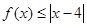 在
在 上恒成立,求
上恒成立,求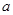 的取值范围。
的取值范围。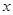 的不等式
的不等式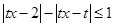 ,其中
,其中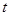 是实参数.
是实参数.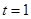 时,解上面的不等式.
时,解上面的不等式.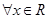 ,上面的不等式均成立,求实数
,上面的不等式均成立,求实数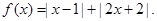
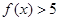 ;
;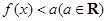 的解集为空集,求
的解集为空集,求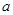 的取值范围.
的取值范围.