题目内容
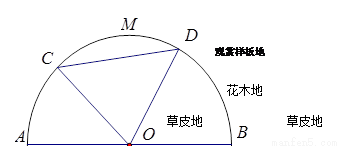
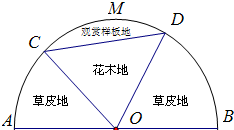 某园林公司计划在一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
某园林公司计划在一块以O为圆心,R(R为常数,单位为米)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.(1)设∠COD=θ(单位:弧度),用θ表示弓形CMDC的面积S弓=f(θ);
(2)园林公司应该怎样规划这块土地,才能使总利润最大?并求相对应的θ.
(参考公式:扇形面积公式S=
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)设∠COD=θ(单位:弧度),利用扇形面积减去三角形的面积,即可求出弓形CMDC的面积S弓=f(θ);
(2)设总利润为y元,草皮利润为y1元,花木地利润为y2,观赏样板地成本为y3,求出y的表达式,利用导数确定函数的最大值,得到结果.
(2)设总利润为y元,草皮利润为y1元,花木地利润为y2,观赏样板地成本为y3,求出y的表达式,利用导数确定函数的最大值,得到结果.
解答:解:(1)S扇=
R2θ,S△OCD=
R2sinθ,S弓=f(θ)=
R2(θ-sinθ).
(2)设总利润为y元,草皮利润为y1元,花木地利润为y2,观赏样板地成本为y3y1=3(
πR2-
R2θ),y2=
R2sinθ•8,y3=
R2(θ-sinθ)•2,
∴y=y1+y2-y3=3(
πR2-
R2θ)+
R2sinθ•8-
R2(θ-sinθ)•2.=
R2[3π-(5θ-10sinθ)]
设g(θ)=5θ-10sinθθ∈(0,π).g′(θ)=5-10cosθg′(θ)<0,cosθ>
,g(θ)在θ∈(0,
)上为减函数;g′(θ)>0,cosθ<
,g(θ)在θ∈(
,π)上为增函数.
当θ=
时,g(θ)取到最小值,此时总利润最大.
答:所以当园林公司把扇形的圆心角设计成
时,总利润最大.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)设总利润为y元,草皮利润为y1元,花木地利润为y2,观赏样板地成本为y3y1=3(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴y=y1+y2-y3=3(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设g(θ)=5θ-10sinθθ∈(0,π).g′(θ)=5-10cosθg′(θ)<0,cosθ>
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
当θ=
| π |
| 3 |
答:所以当园林公司把扇形的圆心角设计成
| π |
| 3 |
点评:本题是中档题,考查三角函数的应用题中的应用,三角函数的化简求值,导数的应用,考查计算能力,转化思想的应用.

练习册系列答案
相关题目
(本小题满分13分)某园林公司计划在一块 为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形
为圆心,半径为5的半圆形(如图)地上种植花草树木,其中弓形 区域用于观赏样板地,
区域用于观赏样板地, 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
(1) 设 ,
, ,分别用
,分别用 ,
, 表示弓形
表示弓形 的面积
的面积 ;
;




|
 (2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式
(2) 园林公司应该怎样规划这块土地,才能使总利润最大?(参考公式:扇形面积公式 )
)
 |
 为圆心,
为圆心, (
(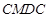 区域用于观赏样板地,
区域用于观赏样板地,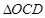 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.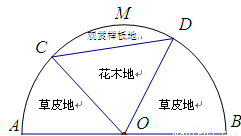
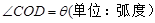 , ,用
, ,用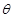 表示弓形
表示弓形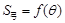 ;
;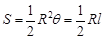 ,
,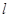 表示扇形的弧长)
表示扇形的弧长)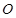 为圆心,
为圆心, (
( 区域用于观赏样板地,
区域用于观赏样板地,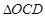 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
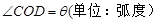 , 用
, 用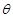 表示弓形
表示弓形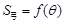 ;(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的
;(2)园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的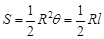 ,
,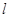 表示扇形的弧长)
表示扇形的弧长) 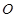 为圆心,
为圆心, (
(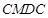 区域用于观赏样板地,
区域用于观赏样板地, 区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.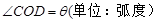 , ,用
, ,用 表示弓形
表示弓形 ;
; ,
, 表示扇形的弧长)
表示扇形的弧长)