题目内容
P，Q 是平面α 内两个定点，点M 为平面α 内的动点，且
=λ （λ＞0，且λ≠1），点M 的轨迹所围成的平面区域的面积为S，设S=f（λ） （λ＞0，且λ≠1），则以下判断正确的是（ ）
| |MP| |
| |MQ| |
| A、f（λ）在（0，1）上是增函数，在（1，+∞）上也是增函数 |
| B、f（λ）在（0，1）上是减函数，在（1，+∞）上也是减函数 |
| C、f（λ）在（0，1）上是增函数，在（1，+∞）上是减函数 |
| D、f（λ）在（0，1）上是减函数，在（1，+∞）上是增函数 |
分析：设：M（x，y），为方便设P（-a，0），Q（a，0）根据|MP|=λ|MQ|建立等式关系，求出轨迹方程，然后点M的轨迹所围成的平面区域的面积为S=f（λ），研究其单调性即可．
解答：解：设：M（x，y），为方便设P（-a，0），Q（a，0）
则：|MP|=λ|MQ|⇒|MP|2=λ2[|MQ|2]⇒（x+a）2+y2=λ2[（x-a）2+y2]⇒
（1-λ2）x2+（1-λ2）y2+2a（1+λ2）x=a2（λ2-1）⇒
x2+y2-2a•
x=-a2⇒其轨迹是个圆．圆的半径是R，则：R2=（2a•
）2-a2
⇒题目中f（x）的单调性就是这个的单调性
设：g（λ）=（2•
）2=4（1+
）2
故选D．
则：|MP|=λ|MQ|⇒|MP|2=λ2[|MQ|2]⇒（x+a）2+y2=λ2[（x-a）2+y2]⇒
（1-λ2）x2+（1-λ2）y2+2a（1+λ2）x=a2（λ2-1）⇒
x2+y2-2a•
| 1+λ2 |
| λ2-1 |
| 1+λ2 |
| λ2-1 |
⇒题目中f（x）的单调性就是这个的单调性
设：g（λ）=（2•
| 1+λ2 |
| λ2-1 |
| 2 |
| λ2-1 |
故选D．
点评：本题主要考查了函数单调性的判断与证明，解题的关键是求轨迹方程，属于中档题．
练习册系列答案
相关题目
（λ＞0，且λ≠1），点M 的轨迹所围成的平面区域的面积为S，设S=f（λ） （λ＞0，且λ≠1），则以下判断正确的是（ ）
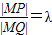（λ＞0，且λ≠1），点M 的轨迹所围成的平面区域的面积为S，设S=f（λ） （λ＞0，且λ≠1），则以下判断正确的是（ ）
（λ＞0，且λ≠1），点M 的轨迹所围成的平面区域的面积为S，设S=f（λ） （λ＞0，且λ≠1），则以下判断正确的是（ ）
（λ＞0，且λ≠1），点M 的轨迹所围成的平面区域的面积为S，设S=f（λ） （λ＞0，且λ≠1），则以下判断正确的是（ ）