题目内容
已知 是等差数列
是等差数列 的前
的前 项和,满足
项和,满足 ;
; 是数列
是数列 的前
的前 项和,满足:
项和,满足: .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
【答案】
(1)数列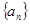 ,
,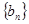 的通项公式分别为
的通项公式分别为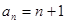 ,
,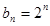 ;(2)
;(2)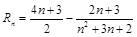 .
.
【解析】
试题分析:(1)由已知条件,首先设;等差数列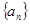 的公差
的公差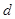 ,列出关于首项和公差
,列出关于首项和公差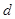 的方程组,解这个方程组,可得
的方程组,解这个方程组,可得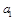 和
和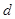 的值,进而可以写出数列
的值,进而可以写出数列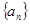 的通项公式.由数列
的通项公式.由数列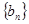 的前
的前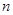 项和
项和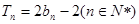 ,写出
,写出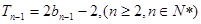 ,两式相减并化简整理,得
,两式相减并化简整理,得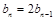 ,从而
,从而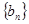 是以2为公比的等比数列,从而可求得数列
是以2为公比的等比数列,从而可求得数列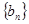 的通项公式;(2)先写出数列
的通项公式;(2)先写出数列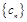 的前
的前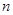 项和
项和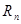 的表达式,分析其结构特征,利用分组求和法及裂项相消法求
的表达式,分析其结构特征,利用分组求和法及裂项相消法求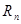 .
.
试题解析:(1)设等差数列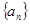 的公差
的公差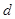 ,则有
,则有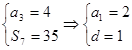 ,所以
,所以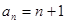 .
.
2分
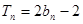 ,
,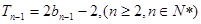 ,两式相减得:
,两式相减得: 且
且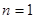 也满足,所以
也满足,所以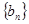 是以2为公比的等比数列,又因为
是以2为公比的等比数列,又因为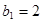 ,所以,
,所以,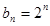 6分
6分
(2)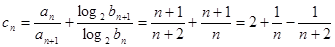 9分
9分
所以: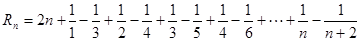
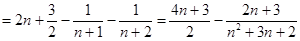 12分
12分
考点:1.等差数列、等比数列的通项公式;2.数列前 项的和.
项的和.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 对称中心是
对称中心是 ;
; 是等差数列
是等差数列 的前
的前 项和,若
项和,若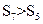 ,则
,则 ;
; 为奇函数的充要条件是
为奇函数的充要条件是 ;[
;[ 均是正数,且
均是正数,且 ,则
,则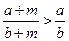 。
。 是等差数列
是等差数列 的前
的前 项和,且
项和,且 ,
,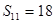 ,则
,则 等于( )
等于( ) 是等差数列
是等差数列 的前
的前 项和,若
项和,若 ,则
,则 的值是( )
的值是( )