题目内容
已知整数n≥4,集合M={1,2,3,…,n}的所有3个元素的子集记为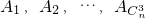 .
.
(1)当n=5时,求集合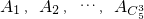 中所有元素之和.
中所有元素之和.
(2)设mi为Ai中的最小元素,设Pn=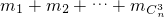 ,试求Pn.
,试求Pn.
解:(1)当n=5时,含元素1的子集中,必有除1以外的两个数字,两个数字的选法有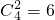 个,所以含有数字1的几何有6个.同理含2,3,4,5的子集也各有6个,
个,所以含有数字1的几何有6个.同理含2,3,4,5的子集也各有6个,
于是所求元素之和为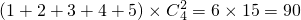 …(5分)
…(5分)
(2)证明:不难得到1≤mi≤n-2,mi∈Z,并且以1为最小元素的子集有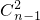 个,以2为最小元素的子集有
个,以2为最小元素的子集有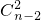 个,以3为最小元素的子集有
个,以3为最小元素的子集有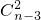 ,…,以n-2为最小元素的子集有
,…,以n-2为最小元素的子集有 个,
个,
则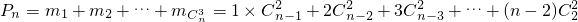 …(8分)
…(8分)
= =
=
= =
=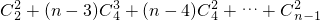
=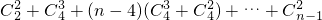 =
=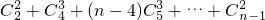
=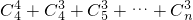 =
= …(10分)
…(10分)
分析:(1)由题意可知集合A中的元素,组成集合A的子集的元素,出现的概率相等,求出每个元素出现的次数,即可求出所有元素的和.
(2)若mi为Ai中的最小元素,则应有1≤mi≤n-2,mi∈Z,若1为某个子集的最小元素,则这样的子集个数有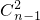 个,若2为某个子集的最小元素,则这个集合中,必不再有1,另外两元素取自剩余的n-2个数字中,有
个,若2为某个子集的最小元素,则这个集合中,必不再有1,另外两元素取自剩余的n-2个数字中,有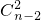 个,,…,以n-2为最小元素的子集有
个,,…,以n-2为最小元素的子集有 个,利用组合数性质
个,利用组合数性质
点评:本题考查了子集的概念,组合的概念及性质,分类讨论的思想方法,考查推理、计算能力.两题中得出含有相关数字出现的次数是关键.
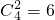 个,所以含有数字1的几何有6个.同理含2,3,4,5的子集也各有6个,
个,所以含有数字1的几何有6个.同理含2,3,4,5的子集也各有6个,于是所求元素之和为
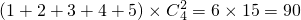 …(5分)
…(5分)(2)证明:不难得到1≤mi≤n-2,mi∈Z,并且以1为最小元素的子集有
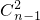 个,以2为最小元素的子集有
个,以2为最小元素的子集有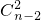 个,以3为最小元素的子集有
个,以3为最小元素的子集有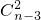 ,…,以n-2为最小元素的子集有
,…,以n-2为最小元素的子集有 个,
个,则
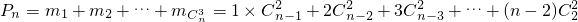 …(8分)
…(8分)=
 =
=
=
 =
=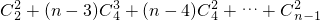
=
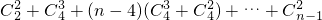 =
=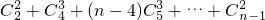
=
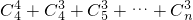 =
= …(10分)
…(10分)分析:(1)由题意可知集合A中的元素,组成集合A的子集的元素,出现的概率相等,求出每个元素出现的次数,即可求出所有元素的和.
(2)若mi为Ai中的最小元素,则应有1≤mi≤n-2,mi∈Z,若1为某个子集的最小元素,则这样的子集个数有
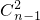 个,若2为某个子集的最小元素,则这个集合中,必不再有1,另外两元素取自剩余的n-2个数字中,有
个,若2为某个子集的最小元素,则这个集合中,必不再有1,另外两元素取自剩余的n-2个数字中,有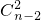 个,,…,以n-2为最小元素的子集有
个,,…,以n-2为最小元素的子集有 个,利用组合数性质
个,利用组合数性质点评:本题考查了子集的概念,组合的概念及性质,分类讨论的思想方法,考查推理、计算能力.两题中得出含有相关数字出现的次数是关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
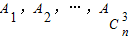 .
.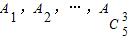 中所有元素之和.
中所有元素之和.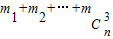 ,试求Pn.
,试求Pn.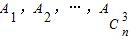 .
.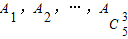 中所有元素之和.
中所有元素之和.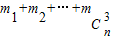 ,试求Pn.
,试求Pn.