题目内容
已知函数 下列结论中①
下列结论中①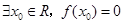 ②函数
②函数 的图象是中心对称图形 ③若
的图象是中心对称图形 ③若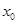 是
是 的极小值点,则
的极小值点,则 在区间
在区间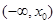 单调递减 ④若
单调递减 ④若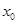 是
是 的极值点,则
的极值点,则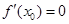 . 正确的个数有( )
. 正确的个数有( )
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:①对于
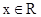 ,当
,当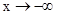 时,
时,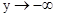 ,当
,当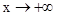 时,
时,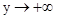 ;∴
;∴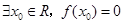 ,命题正确;
,命题正确;
②∵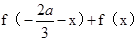 =
=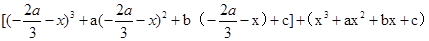
=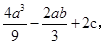

∴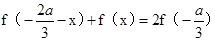 ,∴
,∴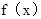 关于点
关于点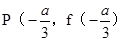 )成中心对称,∴命题正确;
)成中心对称,∴命题正确;
③∵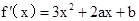 .
.
(i)当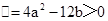 时,
时,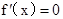 有两解,不妨设为
有两解,不妨设为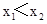 ,列表如下
,列表如下
由表格可知:
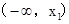
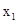
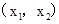
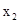
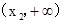

+ 0 - 0 + 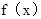
单调递增 极大值 单调递减 极小值 单调递增 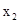 是函数
是函数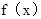 的极小值点,但是
的极小值点,但是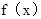 在区间
在区间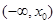 不具有单调性,∴命题不正确;
不具有单调性,∴命题不正确;
(ii)当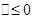 时,
时,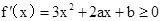 恒成立,∴
恒成立,∴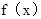 在R上单调增函数,不存在极值点;
在R上单调增函数,不存在极值点;
④由表格可知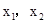 分别为
分别为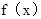 的极值点,且
的极值点,且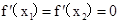 ,∴命题正确.
,∴命题正确.
综上,正确的命题有①②④;
故选C.
考点:应用导数研究函数的单调性、极值

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
设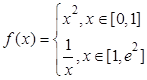 (其中e为自然对数的底数),则
(其中e为自然对数的底数),则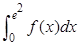 的值为( )
的值为( )
A.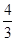 | B.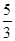 | C.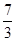 | D.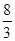 |
若点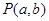 在函数
在函数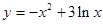 的图像上,点
的图像上,点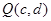 在函数
在函数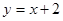 的图像上,则
的图像上,则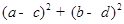 的最小值为( )
的最小值为( )
A.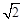 | B.2 | C.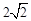 | D.8 |
设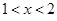 ,则
,则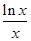 、
、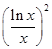 、
、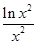 的大小关系是( )
的大小关系是( )
A. | B.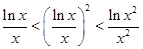 |
C.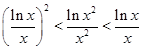 | D.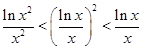 |
已知函数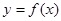 的图象关于原点对称,且当
的图象关于原点对称,且当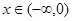 时,
时,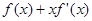
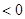 成立,(其中
成立,(其中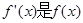 的导函数),若
的导函数),若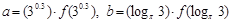 ,
,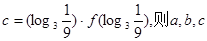 的大小关系是( )
的大小关系是( )
| A.a>b>C | B.c>b>a | C.c>a>b | D.a>c>b |
函数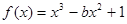 有且仅有两个不同的零点,则
有且仅有两个不同的零点,则 的值为( )
的值为( )
A.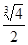 | B.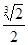 | C.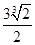 | D.不确定 |
若函数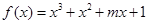 是R上的单调函数,则实数m的取值范围是( )
是R上的单调函数,则实数m的取值范围是( )
A.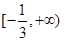 | B.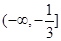 | C.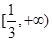 | D.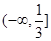  |
曲线 与
与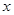 轴以及直线
轴以及直线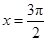 所围图形的面积为( )
所围图形的面积为( )
A.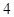 | B.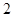 | C.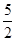 | D.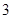 |
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边
长为( )
A.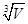 | B.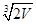 | C.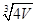 | D.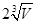 |