题目内容
若cos α+2sin α=- ,则tan α=________.
,则tan α=________.
2
分析:利用辅角公式求得sin(α+φ)的值,进而利用正弦函数的性质求得α+φ的值,进而利用同角三角函数的基本关系和诱导公式求得tanα.
解答:由已知得 sin(α+φ)=-
sin(α+φ)=- (其中tanφ=
(其中tanφ= ),
),
即有sin(α+φ)=-1,
所以α+φ=2kπ- ,α=2kπ-
,α=2kπ- -φ(k∈Z),
-φ(k∈Z),
所以tanα=tan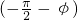 =
= =2.
=2.
故答案为:2
点评:本题主要考查了同角三角函数的基本关系的应用和诱导公式的化简求值.考查了基础知识的理解和应用.
分析:利用辅角公式求得sin(α+φ)的值,进而利用正弦函数的性质求得α+φ的值,进而利用同角三角函数的基本关系和诱导公式求得tanα.
解答:由已知得
 sin(α+φ)=-
sin(α+φ)=- (其中tanφ=
(其中tanφ= ),
),即有sin(α+φ)=-1,
所以α+φ=2kπ-
 ,α=2kπ-
,α=2kπ- -φ(k∈Z),
-φ(k∈Z),所以tanα=tan
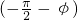 =
= =2.
=2.故答案为:2
点评:本题主要考查了同角三角函数的基本关系的应用和诱导公式的化简求值.考查了基础知识的理解和应用.

练习册系列答案
相关题目
若cosα+2sinα=-
,则tanα=( )
| 5 |
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |