题目内容
已知一组数x1,x2,x3,x4的平均数是
=1,方差s2=2,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )
. |
| x |
分析:根据x1,x2,x3,x4的平均数是1,方差是2,可计算出x1+x2+x3+x4、x12+x22+x32+x42值,代入另一组的平均数和方差的计算公式即可.
解答:解:由题知,x1+x2+x3+x4=1×4=4,
S12=
[(x1-1)2+(x2-1)2+(x3-1)2+(x4-1)2]
=
[(x12+x22+x32+x42)-2(x1+x2+x3+x4)+1×4]=2,
∴x12+x22+x32+x42=12.
另一组数据的平均数=
[2x1+1+2x2+1+2x3+1+2x4+1]=
[2(x1+x2+x3+x4)+1×4]=
[2×4+4]=3,
另一组数据的方差=
[(2x1+1-3)2+(2x2+1-3)2+(2x3+1-3)2+(2x4+1-3)2]
=
[4(x12+x22+x32+x42)-8(x1+x2+x3+x4)+4×4]=
[4×12-32+16]=8.
故选B.
S12=
| 1 |
| 4 |
=
| 1 |
| 4 |
∴x12+x22+x32+x42=12.
另一组数据的平均数=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
另一组数据的方差=
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 4 |
故选B.
点评:本题主要考查了平均数、方差的计算.关键是熟悉计算公式,会将所求式子变形,再整体代入,属于基础题.

练习册系列答案
相关题目
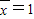 ,方差s2=2,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )
,方差s2=2,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )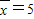 ,方差s2=4,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )
,方差s2=4,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )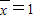 ,方差s2=2,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )
,方差s2=2,则数据2x1+1,2x2+1,2x3+1,2x4+1的平均数和方差分别是( )