题目内容
已知函数 .
.
(1)当x≥1时,证明:不等式f(x)≤x+lnx恒成立;
(2)若数列{an}满足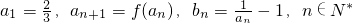 ,证明数列{bn}是等比数列,并求出数列{bn}、{an}的通项公式;
,证明数列{bn}是等比数列,并求出数列{bn}、{an}的通项公式;
(3)在(2)的条件下,若cn=an•an+1•bn+1(n∈N+),证明:c1+c2+c3+…cn< .
.
解:(1)方法一:∵x≥1,∴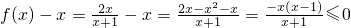
而x≥1时,lnx≥0∴x≥1时,f(x)-x≤lnx,∴当x≥1时,f(x)≤x+lnx恒成立.
方法二:令φ(x)=f(x)-x-lnx(x≥1),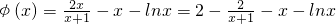 ,
,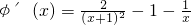 ,∵x≥1,∴
,∵x≥1,∴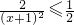 ,∴
,∴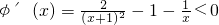 ,
,
故φ(x)是定义域[1,+∞)上的减函数,∴当x≥1时,φ(x)≤φ(1)=0恒成立.
即当x≥1时,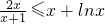 恒成立.∴当x≥1时,f(x)≤x+lnx恒成立.(4分)
恒成立.∴当x≥1时,f(x)≤x+lnx恒成立.(4分)
(2)an+1=f(an),∴ ,∵
,∵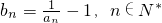 ,
,
∴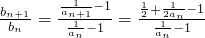 =
=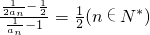 ,
,
又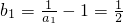 ,∴bn是首项为
,∴bn是首项为 ,公比为
,公比为 的等比数列,其通项公式为
的等比数列,其通项公式为 .
.
又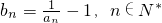 ,
,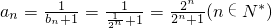 .(10分)
.(10分)
(3)cn=an•an+1•bn+1=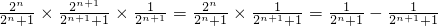 ,
,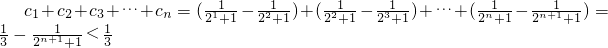 .
.
分析:(1)方法一:先证明f(x)-x≤0,再证明lnx≥0,从而不等式f(x)≤x+lnx恒成立.
方法二:构造函数φ(x)=f(x)-x-lnx;利用导数判断单调性,求出函数最大值φ(1),而φ(1)=0,从而不等式恒成立.
(2)先利用an+1=f(an)通过取倒数变形,然后根据等比数列的定义,求出公比,从而证得.
(3)利用(2)问中求出的{an}的通项公式,代入cn=an•an+1•bn+1中,并用分离法拆成两项之差,然后用叠加法即可解答.
点评:此题考查函数导数的应用,等比数列常规证明及裂项后用叠加的方法.
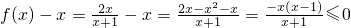
而x≥1时,lnx≥0∴x≥1时,f(x)-x≤lnx,∴当x≥1时,f(x)≤x+lnx恒成立.
方法二:令φ(x)=f(x)-x-lnx(x≥1),
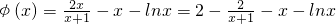 ,
,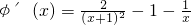 ,∵x≥1,∴
,∵x≥1,∴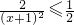 ,∴
,∴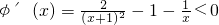 ,
,故φ(x)是定义域[1,+∞)上的减函数,∴当x≥1时,φ(x)≤φ(1)=0恒成立.
即当x≥1时,
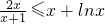 恒成立.∴当x≥1时,f(x)≤x+lnx恒成立.(4分)
恒成立.∴当x≥1时,f(x)≤x+lnx恒成立.(4分)(2)an+1=f(an),∴
 ,∵
,∵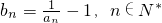 ,
,∴
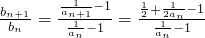 =
=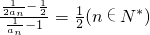 ,
,又
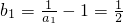 ,∴bn是首项为
,∴bn是首项为 ,公比为
,公比为 的等比数列,其通项公式为
的等比数列,其通项公式为 .
.又
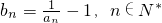 ,
,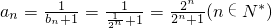 .(10分)
.(10分)(3)cn=an•an+1•bn+1=
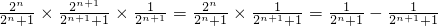 ,
,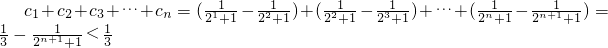 .
.分析:(1)方法一:先证明f(x)-x≤0,再证明lnx≥0,从而不等式f(x)≤x+lnx恒成立.
方法二:构造函数φ(x)=f(x)-x-lnx;利用导数判断单调性,求出函数最大值φ(1),而φ(1)=0,从而不等式恒成立.
(2)先利用an+1=f(an)通过取倒数变形,然后根据等比数列的定义,求出公比,从而证得.
(3)利用(2)问中求出的{an}的通项公式,代入cn=an•an+1•bn+1中,并用分离法拆成两项之差,然后用叠加法即可解答.
点评:此题考查函数导数的应用,等比数列常规证明及裂项后用叠加的方法.

练习册系列答案
相关题目
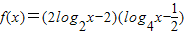 .
.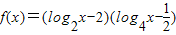 .
.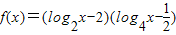 .
.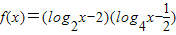 .
.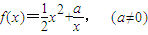 .
.