题目内容
在如下数表中,已知每行、每列中的数都成等差数列,那么,位于下表中的第n行第n+1列的数是 .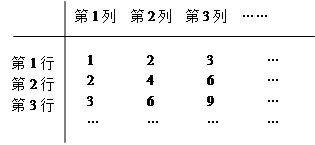
n+n2.
解析试题分析:从表格可知,第n行的等差数列的首项为n,公差也为n,根据等差数列的通项公式,其位于第n+1个数是n+(n-1)n= n+n2,所以位于下表中的第n行第n+1列的数是n+n2.
考点:等差数列的通项公式,观察与归纳的能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知等差数列 前
前 项和为
项和为 ,
, ,
, 210,
210, 130,则
130,则 = ( )
= ( )
| A.12 | B.14 | C.16 | D.18 |
两等差数列{an}、{bn}的前n项和的比 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
等差数列{an}中,前n项的和为Sn,若a7=1,a9=5,那么S15等于( )
| A.90 | B.45 | C.30 | D.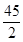 |
 、
、 的前项和分别为
的前项和分别为 和
和 ,若
,若 ,则
,则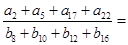 .
. 中,前
中,前 项和
项和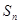 ,若
,若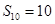 ,
,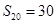 ,则
,则 = .
= .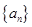 的前
的前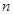 项和为
项和为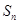 ,且
,且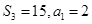 ,则
,则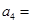 ______.
______.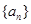 的前
的前 项和为
项和为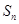 ,若
,若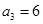 ,
,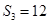 ,则公差
,则公差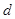 等于 .
等于 .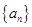 是公差不为零的等差数列,
是公差不为零的等差数列,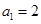 且
且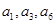 成等比数列,则
成等比数列,则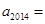 .
.