题目内容
设 ,若直线
,若直线 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于点
轴相交于点 ,且坐标原点
,且坐标原点 到直线
到直线 的距离为
的距离为 ,则
,则 的面积
的面积 的最小值为
的最小值为
A.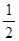 | B.2 | C.3 | D.4 |
C
解析试题分析:原点 到直线
到直线 的距离
的距离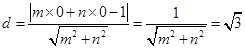 ,
,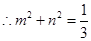 ,在直线
,在直线 的方程中,令
的方程中,令 可得
可得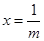 ,即直线
,即直线 与
与 轴交于点
轴交于点 ,令
,令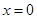 可得
可得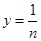 ,即直线
,即直线 与
与 轴交于点
轴交于点 ,
, ,当且仅当
,当且仅当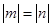 时上式取等号,由于
时上式取等号,由于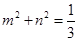 ,故当
,故当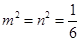 时,
时,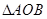 面积取最小值
面积取最小值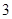 .
.
考点:原点 到直线
到直线 的距离
的距离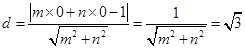 ,
,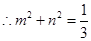 ,在直线
,在直线 的方程中,令
的方程中,令 可得
可得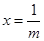 ,即直线
,即直线 与
与 轴交于点
轴交于点 ,令
,令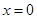 可得
可得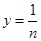 ,即直线
,即直线 与
与 轴交于点
轴交于点 ,
, ,当且仅当
,当且仅当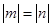 时上式取等号,由于
时上式取等号,由于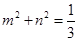 ,故当
,故当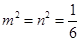 时,
时,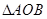 面积取最小值
面积取最小值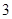 .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
若正数 满足
满足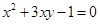 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C.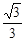 | D. |
下列命题错误的是( )
A.若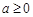 , ,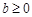 ,则 ,则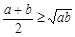 |
B.若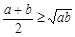 ,则 ,则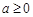 , ,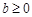 |
C.若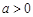 , ,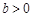 ,且 ,且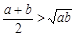 ,则 ,则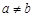 |
D.若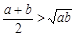 ,且 ,且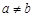 ,则 ,则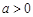 , ,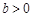 |
“a>b>0”是“ab< ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若实数 、
、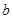 、
、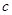 、
、 满足
满足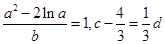 ,则
,则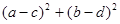 的最小值 为 ( )
的最小值 为 ( )
A.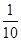 | B.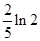 | C.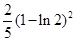 | D.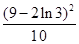 |
若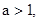 则
则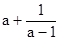 的最小值是 ( )
的最小值是 ( )
| A.2 | B.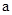 | C.3 | D.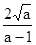 |
已知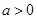 ,
,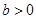 ,
,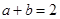 ,则
,则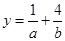 的最小值是 ( )
的最小值是 ( )
A.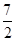 | B.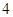 | C.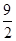 | D.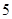 |
已知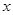 ,
, ,且
,且 ,则
,则 的最大值是( )
的最大值是( )
| A.3 | B.3.5 | C.4 | D.4.5 |
 ,则
,则 的最小值为 .
的最小值为 .