题目内容
已知a ≥ ,f(x)=-a2x2+ax+c.
,f(x)=-a2x2+ax+c.
(1)如果对任意x∈[0,1],总有f(x)≤1成立, 证明c≤ ;
;
(2)已知关于x的二次方程f(x)=0有两个不等实根 ,
, ,且
,且 ,求实数c的取值范围
,求实数c的取值范围
【答案】
(1)f(x)=-a2(x-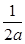 )2+c+
)2+c+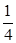 ,
,
∵a≥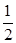 ,∴
,∴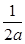 ∈(0,1
∈(0,1 ,
,
∴x∈(0,1 时,[f(x)]max=c+
时,[f(x)]max=c+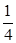 ,---------------------2分
,---------------------2分
∵f(x)≤1,则[f(x)]max=c+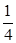 ≤1,即c≤
≤1,即c≤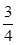 ,
,
∴对任意x∈[0,1],总有f(x)≤1成立时,可得c≤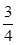 .---------5分
.---------5分
(2)∵a≥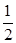 ,∴
,∴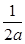 >0
>0
又抛物线开口向下,f(x)=0的两根在[0,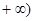 内,
内,

所求实数c的取值范围为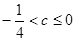 。
。
【解析】略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知a是函数f(x)=2x-log
x的零点,若0<x0<a,则f(x0)的值满足( )
| 1 |
| 2 |
| A、f(x0)=0 |
| B、f(x0)>0 |
| C、f(x0)<0 |
| D、f(x0)的符号不确定 |