题目内容
在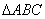 中,角
中,角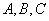 的对边分别为
的对边分别为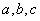 ,若
,若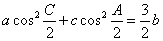 .
.
(Ⅰ)求证: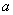 、
、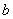 、
、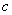 成等差数列;
成等差数列;
(Ⅱ)若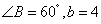 ,求
,求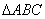 的面积.
的面积.
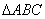 中,角
中,角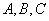 的对边分别为
的对边分别为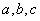 ,若
,若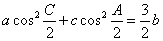 .
.(Ⅰ)求证:
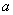 、
、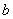 、
、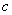 成等差数列;
成等差数列;(Ⅱ)若
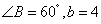 ,求
,求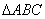 的面积.
的面积.(1)根据已知的边角关系,结合二倍角公式来化简得到证明。
(2)
(2)

试题分析:(1)证明:

即

由正弦定理得:

即


由正弦定理:
整理得:
 ,故
,故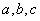 成等差数列
成等差数列(2)由
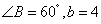 及余弦定理得:
及余弦定理得:
∴

又由(1)知
 ,可得
,可得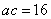
∴
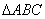 的面积
的面积
点评:主要是考查了正弦定理和余弦定理以及等差数列的综合运用 ,属于中档题。

练习册系列答案
相关题目
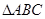 的周长为
的周长为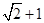 ,且
,且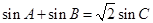 ,
,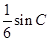 ,求角C的度数。
,求角C的度数。 中,
中, 分别为角
分别为角 所对的边,若
所对的边,若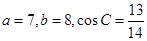 ,则
,则 .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,则
,则 __________
__________ km,再朝西偏北
km,再朝西偏北 的方向走了3km,结果它离出发点恰好为
的方向走了3km,结果它离出发点恰好为 km,那么
km,那么 C.3 D.
C.3 D.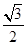 ,则这个三角形的面积是 。
,则这个三角形的面积是 。 ,则角
,则角 的值是 .
的值是 . 中,角
中,角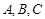 所对的边分别为
所对的边分别为 ,若
,若 。
。 ;
; 的平分线交
的平分线交 于
于 ,且
,且 ,求
,求 的值。
的值。 +cos A=0.
+cos A=0. ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.