题目内容
水库的蓄水量随时间而变化,现用t表示时间(单位:月),以年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为v(t)=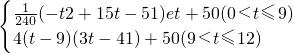 .
.
(1)若该水库的蓄水量小于50的时期称为枯水期,以i-1<t≤i表示第i月份(i=1,2,…12),问一年内那几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取e3=20计算).
解:(1)当0<t≤9时,v(t)=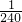 (-t2+15t-51)et+50<50,
(-t2+15t-51)et+50<50,
即t2-15t+51>0,
解得t> 或t<
或t< ,
,
从而0<t< ≈5.2.
≈5.2.
当9<t≤12时,v(t)=4(t-9)(3t-41)+50<50,
即(t-9)(3t-41)<0,
解得9<t< ,所以9<t≤12.
,所以9<t≤12.
综上,0<t<5.2或9<t≤12,枯水期为1,2,3,4,5,10,11,12月.
(2)由(1)知,水库的最大蓄水量只能在6~9月份.
v′(t)=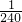 (-t2+13t-36)et=-
(-t2+13t-36)et=-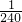 et(t-1)(t-9),
et(t-1)(t-9),
令v′(t)=0,解得t=9或t=4(舍去),
又当t∈(6,9)时,v′(t)>0;当t∈(9,10)时,v′(t)<0.
所以,当t=9时,v(t)的最大值v(9)=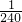 ×3×e9+50=150(亿立方米),
×3×e9+50=150(亿立方米),
故一年内该水库的最大蓄水量是150亿立方米.
分析:(1)对t分段讨论,分别令v(t)<0,解不等式求出t的范围即得到枯水期对应的月份.
(2)据(1)判断出最大值所在的可能月份,求出v(t)的导数,求出导函数大于0和小于0的t的范围即函数的单调区间,求出最值.
点评:解决分段函数的有关问题,有关分段研究,再将求出的结果求并集;解决实际问题,要注意最后将数学问题还原到实际问题.
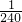 (-t2+15t-51)et+50<50,
(-t2+15t-51)et+50<50,即t2-15t+51>0,
解得t>
 或t<
或t< ,
,从而0<t<
 ≈5.2.
≈5.2.当9<t≤12时,v(t)=4(t-9)(3t-41)+50<50,
即(t-9)(3t-41)<0,
解得9<t<
 ,所以9<t≤12.
,所以9<t≤12.综上,0<t<5.2或9<t≤12,枯水期为1,2,3,4,5,10,11,12月.
(2)由(1)知,水库的最大蓄水量只能在6~9月份.
v′(t)=
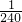 (-t2+13t-36)et=-
(-t2+13t-36)et=-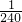 et(t-1)(t-9),
et(t-1)(t-9),令v′(t)=0,解得t=9或t=4(舍去),
又当t∈(6,9)时,v′(t)>0;当t∈(9,10)时,v′(t)<0.
所以,当t=9时,v(t)的最大值v(9)=
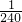 ×3×e9+50=150(亿立方米),
×3×e9+50=150(亿立方米),故一年内该水库的最大蓄水量是150亿立方米.
分析:(1)对t分段讨论,分别令v(t)<0,解不等式求出t的范围即得到枯水期对应的月份.
(2)据(1)判断出最大值所在的可能月份,求出v(t)的导数,求出导函数大于0和小于0的t的范围即函数的单调区间,求出最值.
点评:解决分段函数的有关问题,有关分段研究,再将求出的结果求并集;解决实际问题,要注意最后将数学问题还原到实际问题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
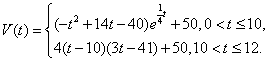
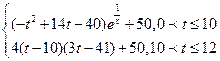 。
。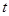 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于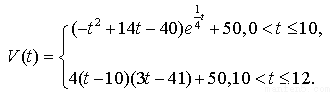
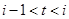 表示第
表示第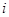 月份(
月份(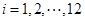 ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?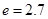 计算)。
计算)。