题目内容
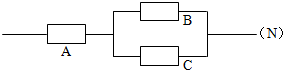
8、如图，用A，B，C三个不同的元件连接成一个系统N．当元件A正常工作且元件B、C至少有一个正常工作时，系统N正常工作．已知元件A，B，C正常工作的概率依次为0.8，0.85，0.9，则系统N能正常工作的概率等于
0.788
．分析：由题意用A，B，C三个不同的元件连接成一个系统N．当元件A正常工作且元件B、C至少有一个正常工作时，系统N正常工作．先算出B，C至少有一个通的概率，再利用乘法原理求值
解答：解：B、C都不工作的概率为（1-0.85）（1-0.9）=0.015
故B、C至少有一个正常工作的概率是0.985
又元件A正常工作的概率依次为0.8
故系统N能正常工作的概率等于0.8×0.985=0.788
故答案为0.788
故B、C至少有一个正常工作的概率是0.985
又元件A正常工作的概率依次为0.8
故系统N能正常工作的概率等于0.8×0.985=0.788
故答案为0.788
点评：本题考查相互独立事件的概率乘法公式，解题的关键是求出B，C所组成的系统能正确常工作的概率，理解并掌握乘法原理是解答本题的知识保证．本题属于概率的应用题，是近几年高考概率的考试方向．
练习册系列答案
相关题目
如图所示，直三棱柱ABC-A1B1C1中，AB⊥AC，D，E分别为AA1，B1C的中点，若记
三个城市分别位于A，B，C三点处（如图），且
斜三棱柱OAB-CA1B1，其中向量