题目内容
已知函数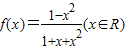 .
.(Ⅰ)求函数f(x)的单调区间和极值;
(Ⅱ)若(et+2)x2+etx+et-2≥0对满足|x|≤1的任意实数x恒成立,求实数t的取值范围(这里e是自然对数的底数);
(Ⅲ)求证:对任意正数a、b、λ、μ,恒有
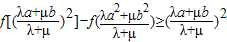
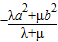 .
.
【答案】分析:(Ⅰ)对函数求导,利用导数可判断函数的单独区间,进而可求函数的极大值,极小值.
(Ⅱ)原不等式可化为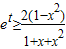 由(Ⅰ)知,|x|≤1时,f(x)的最大值为
由(Ⅰ)知,|x|≤1时,f(x)的最大值为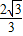 .则可得
.则可得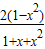 的最大值为
的最大值为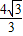 ,由恒成立的意义知道
,由恒成立的意义知道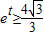 ,从而可求t.
,从而可求t.
(Ⅲ)设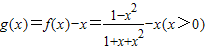 ,对g(x)求导可判断g(x)在(0,+∞)上是减函数,而作差可证明
,对g(x)求导可判断g(x)在(0,+∞)上是减函数,而作差可证明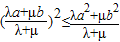 .由g(x)的单调性可证.
.由g(x)的单调性可证.
解答:解:(Ⅰ)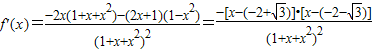
∴f(x)的增区间为 ,f(x)减区间为
,f(x)减区间为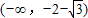 和
和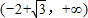 .
.
极大值为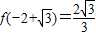 ,极小值为
,极小值为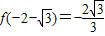 .…4分
.…4分
(Ⅱ)原不等式可化为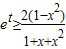 由(Ⅰ)知,|x|≤1时,f(x)的最大值为
由(Ⅰ)知,|x|≤1时,f(x)的最大值为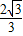 .
.
∴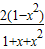 的最大值为
的最大值为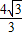 ,由恒成立的意义知道
,由恒成立的意义知道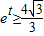 ,从而
,从而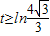 …8分
…8分
(Ⅲ)设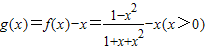
则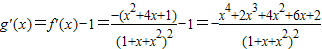 .
.
∴当x>0时,g'(x)<0,故g(x)在(0,+∞)上是减函数,
又当a、b、λ、μ是正实数时,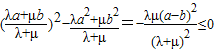
∴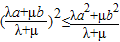 .
.
由g(x)的单调性有: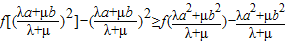 ,
,
即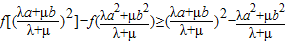 .…12分
.…12分
点评:本题主要考查了函数的恒成立问题的转化的应用,解题的关键是熟练应用导数的知识判断函数的单调性、求解函数的极值及最值及综合应用函数知识求解问题的综合能力
(Ⅱ)原不等式可化为
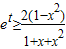 由(Ⅰ)知,|x|≤1时,f(x)的最大值为
由(Ⅰ)知,|x|≤1时,f(x)的最大值为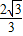 .则可得
.则可得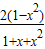 的最大值为
的最大值为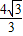 ,由恒成立的意义知道
,由恒成立的意义知道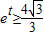 ,从而可求t.
,从而可求t.(Ⅲ)设
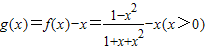 ,对g(x)求导可判断g(x)在(0,+∞)上是减函数,而作差可证明
,对g(x)求导可判断g(x)在(0,+∞)上是减函数,而作差可证明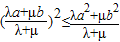 .由g(x)的单调性可证.
.由g(x)的单调性可证.解答:解:(Ⅰ)
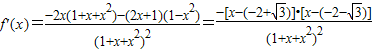
∴f(x)的增区间为
 ,f(x)减区间为
,f(x)减区间为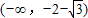 和
和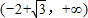 .
.极大值为
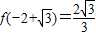 ,极小值为
,极小值为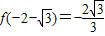 .…4分
.…4分(Ⅱ)原不等式可化为
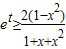 由(Ⅰ)知,|x|≤1时,f(x)的最大值为
由(Ⅰ)知,|x|≤1时,f(x)的最大值为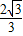 .
.∴
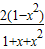 的最大值为
的最大值为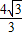 ,由恒成立的意义知道
,由恒成立的意义知道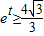 ,从而
,从而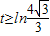 …8分
…8分(Ⅲ)设
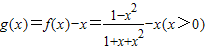
则
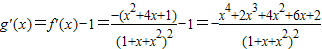 .
.∴当x>0时,g'(x)<0,故g(x)在(0,+∞)上是减函数,
又当a、b、λ、μ是正实数时,
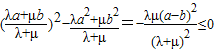
∴
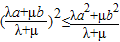 .
.由g(x)的单调性有:
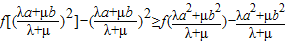 ,
,即
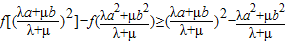 .…12分
.…12分点评:本题主要考查了函数的恒成立问题的转化的应用,解题的关键是熟练应用导数的知识判断函数的单调性、求解函数的极值及最值及综合应用函数知识求解问题的综合能力

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知函数 .
.
(1)求 的最小值;
的最小值;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设 ,试问函数
,试问函数 在
在 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数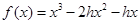 ,若
,若 且
且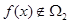 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得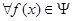 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


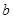
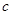




 ,编写一个程序求函数值.
,编写一个程序求函数值. 试画出求函数值的程序框图.
试画出求函数值的程序框图.