题目内容
已知等差数列有一性质：若{an}为等差数列，则通项为bn=| a1+a2+a3+…+an | n |
分析：条件bn=
，根据等差与等比的类比，等差中和对应等比中积，等差中除对应等比中的开方很快得到
| a1+a2+a3+…+an |
| n |
| n | a1a2a3…an |
解答：解：等差数列中算术平均数
，对应等比数列中的几何平均数
，推广算术平均数bn=
对应着几何平均数
，故答案为
| a+b |
| 2 |
| ab |
| a1+a2+a3+…+an |
| n |
| n | a1a2a3…an |
| n | a1a2a3…an |
点评：本题考查了等差与等比之间的类比，和对积，积对乘方等
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
的数列{bn}也是等差数列，类似上述命题，相应的等比数列有性质：若{an}是等比数列(an＞0)，则通项为bn＝________的数列{bn}也是等比数列．
的数列{bn}也是等差数列，类似上述命题，相应的等比数列有性质：若{an}是等比数列（an＞0）,则通项为bn=__________的数列{bn}也是等比数列.
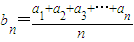的数列{bn}也是等差数列．类比此命题，相应地等比数列有如下性质：若{an}为等比数列（各项均为正），则通项为bn= 的数列{bn}也是等比数列．
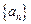是等差数列，则通项为
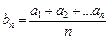的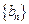
也是等差数列，类似上述命题，相应的等比数列有性质：若
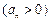，则通项为
=__
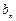__________的数列