题目内容
令 ,则a,b,c的大小关系为 .
,则a,b,c的大小关系为 .
【答案】分析:要比较三个数字的大小,可将a,b,c与中间值0,1进行比较,或利用指数函数与对数函数的性质即可判断,从而确定大小关系.
解答:解:∵y=2x是R上的增函数,又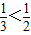 ,
,
∴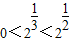
∴0<b<c,
又y=log2x为(0,+∞)上的增函数,
∴a=log2 <log31=0,
<log31=0,
∴a<b<c.
故答案为:a<b<c
点评:本题主要考查了对数值、指数值大小的比较,常常与中间值进行比较,还考查学生掌握与应用指数函数与对数函数的单调性质,属于容易题.
解答:解:∵y=2x是R上的增函数,又
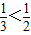 ,
,∴
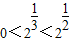
∴0<b<c,
又y=log2x为(0,+∞)上的增函数,
∴a=log2
 <log31=0,
<log31=0,∴a<b<c.
故答案为:a<b<c
点评:本题主要考查了对数值、指数值大小的比较,常常与中间值进行比较,还考查学生掌握与应用指数函数与对数函数的单调性质,属于容易题.

练习册系列答案
相关题目
令a=tanθ,b=sinθ,c=cosθ,若在集合{θ|-
<θ<
,θ≠0,
,
}中,给θ取一个值,a,b,c三数中最大的数是b,则θ的值所在范围是( )
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
A、(-
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
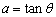 ,
,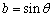 ,
,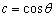 ,若在集合
,若在集合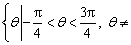
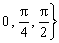 中,给
中,给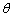 取一个值,
取一个值,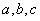 三数中最大的数是
三数中最大的数是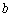 ,则
,则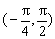 B.
B.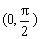 C.
C.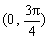 D.
D.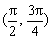
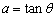 ,
,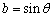 ,
,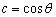 ,若在集合
,若在集合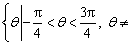
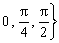 中,给
中,给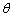 取一个值,
取一个值,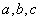 三数中最大的数是
三数中最大的数是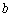 ,则
,则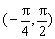 B.
B.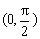 C.
C.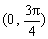 D.
D.