题目内容
一次随堂测验由4道选择题、4道填空题、2道解答题构成,在每道选择题给出的4个备选答案中,只有一个是正确的.某学生在测验中对4道选择题中的每一道都任意选定一个答案,求这4道选择题中:(Ⅰ)恰有两道题答对的概率;
(Ⅱ)至少答对一道题的概率.
【答案】分析:(1)由题意知这是4次独立重复试验,每次试验中事件发生的概率均为定值.得到本实验符合独立重复试验,根据独立重复试验的概率计算公式得到结果.
(2)至少有一道题答对包括答对一道题目,答对两道题目,答对三道题目,答对四道题目,这四种情况是互斥的,根据互斥事件的概率和独立重复试验的概率公式得到结果.
解答:解:视“选择每道题的答案”为一次试验,则这是4次独立重复试验,
且每次试验中“选择正确”这一事件发生的概率均为 .
.
由独立重复试验的概率计算公式得:
(1)恰有两道题答对的概率为
P4(2)=C24( )2(
)2( )2=
)2= .
.
(2)至少有一道题答对包括答对一道题目,答对两道题目,
答对三道题目,答对四道题目,这四种情况是互斥的,
∴至少答对一道题的概率C14( )(
)( )3+C24(
)3+C24( )2(
)2( )2+C34(
)2+C34( )3(
)3( )+C44•(
)+C44•( )4•(
)4•( )
)
= +
+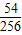 +
+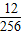 +
+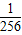 =
=
点评:本题考查独立重复试验,是一个含有”至少“的问题,解题时出来列举出所有的情况,还可以利用对立事件的概率解至少有一道题答对的结果.
(2)至少有一道题答对包括答对一道题目,答对两道题目,答对三道题目,答对四道题目,这四种情况是互斥的,根据互斥事件的概率和独立重复试验的概率公式得到结果.
解答:解:视“选择每道题的答案”为一次试验,则这是4次独立重复试验,
且每次试验中“选择正确”这一事件发生的概率均为
 .
.由独立重复试验的概率计算公式得:
(1)恰有两道题答对的概率为
P4(2)=C24(
 )2(
)2( )2=
)2= .
.(2)至少有一道题答对包括答对一道题目,答对两道题目,
答对三道题目,答对四道题目,这四种情况是互斥的,
∴至少答对一道题的概率C14(
 )(
)( )3+C24(
)3+C24( )2(
)2( )2+C34(
)2+C34( )3(
)3( )+C44•(
)+C44•( )4•(
)4•( )
)=
 +
+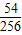 +
+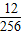 +
+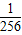 =
=
点评:本题考查独立重复试验,是一个含有”至少“的问题,解题时出来列举出所有的情况,还可以利用对立事件的概率解至少有一道题答对的结果.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目