题目内容
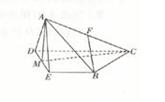
在四棱锥 A-BCDE中,底面是直角梯形,其中 BC∥DE,∠BCD=90°,且 DE=CD=| 1 |
| 2 |
| 1 |
| 2 |
求证:面ABE⊥面BCD.
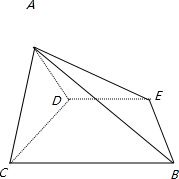
分析:取BE的中点M,CD的中点N,连接 AM,AN,MN,由等腰三角形可得AM⊥BE,AN⊥CD,在直角梯形BCDE中,由中位线可得MN∥BC,
而∠BCD=90°即MN⊥CD,所以CD⊥面AMN,CD⊥AM,AM⊥BE,由线面垂直的判定定理可得 AM⊥面BCD,进而得到面面垂直.
而∠BCD=90°即MN⊥CD,所以CD⊥面AMN,CD⊥AM,AM⊥BE,由线面垂直的判定定理可得 AM⊥面BCD,进而得到面面垂直.
解答: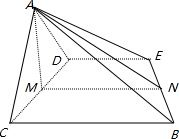 证明:取BE的中点M,CD的中点N,连接 AM,AN,MN,
证明:取BE的中点M,CD的中点N,连接 AM,AN,MN,
∵AB=AC
∴AM⊥BE 同理 AC=AD 有AN⊥CD
在直角梯形BCDE中,
∵M、N分别是BE、CD的中点
∴MN∥BC
又∵∠BCD=90°
∴MN⊥CD
∴CD⊥面AMN
∴CD⊥AM
又∵AM⊥BE,CD、BE 是梯形的两个腰,即它们一定相交,
∴AM⊥面BCD,又AM?面ABE
∴面ABE⊥面BCD.
 证明:取BE的中点M,CD的中点N,连接 AM,AN,MN,
证明:取BE的中点M,CD的中点N,连接 AM,AN,MN,∵AB=AC
∴AM⊥BE 同理 AC=AD 有AN⊥CD
在直角梯形BCDE中,
∵M、N分别是BE、CD的中点
∴MN∥BC
又∵∠BCD=90°
∴MN⊥CD
∴CD⊥面AMN
∴CD⊥AM
又∵AM⊥BE,CD、BE 是梯形的两个腰,即它们一定相交,
∴AM⊥面BCD,又AM?面ABE
∴面ABE⊥面BCD.
点评:本题主要考查线线,线面,面面垂直关系的转化与应用,考查的重点是垂直的判定定理和性质定理,是常考类型,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =45
=45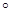 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2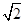 ,
,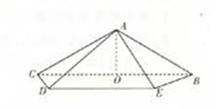
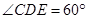 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,