题目内容
（平）若二次函数y=ax2+bx+c（ac≠0）图象的顶点坐标为
，与x轴的交点P、Q位于y轴的两侧，以线段PQ为直径的圆与y轴交于M（0，4）和N（0，-4）．则点（b，c）所在曲线为（ ）A．圆
B．椭圆
C．双曲线
D．抛物线
【答案】分析：确定以线段PQ为直径的圆的圆心坐标，利用|CM|=|CQ|，及二次函数y=ax2+bx+c（ac≠0）图象的顶点坐标，化简，即可求得点（b，c）所在曲线．
解答：解：由题意，以线段PQ为直径的圆的圆心坐标为C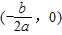
，则
由|CM|=|CQ|，可得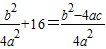
∵二次函数y=ax2+bx+c（ac≠0）图象的顶点坐标为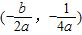
，
∴
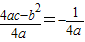
∴b2-4ac=1
∴b2+64a2=1，a=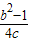
∴
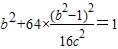
∴c2+4b2=4
∴b2+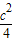
=1
∴点（b，c）所在曲线为椭圆
故选B．
点评：本题考查轨迹方程，考查学生的运算能力，解题的关键是建立等式|CM|=|CQ|，正确化简．
解答：解：由题意，以线段PQ为直径的圆的圆心坐标为C
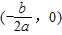，则由|CM|=|CQ|，可得
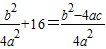
∵二次函数y=ax2+bx+c（ac≠0）图象的顶点坐标为
，∴
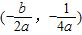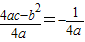
∴b2-4ac=1
∴b2+64a2=1，a=
∴
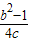
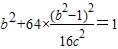
∴c2+4b2=4
∴b2+
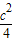=1∴点（b，c）所在曲线为椭圆
故选B．
点评：本题考查轨迹方程，考查学生的运算能力，解题的关键是建立等式|CM|=|CQ|，正确化简．
练习册系列答案
相关题目